The need for complex types in XML schema languages

Sean left a comment referring to a post by James Clark on TEDI, a new kind of schema language for XML. It's a very interesting post. I like how it elevates the issue to one of defining a common data meta-model, with mappings to the plethora of formats which are all basically trying to do the same thing (XML, JSON, YAML, etc).

However, I think I noticed something missing in the TEDI concept. This is the ability to define complex types which are composed of combinations of basic data structures. XML Schema of course does have this feature, and it's responsible for a significant part of the perceived complexity. But a schema language which lacks this ability is limited in its expressiveness. A sterling example is GML Geometry. Geometric types are complex enough that they have to be defined in terms of simpler XML data structures. One of the goals of GML is to provide a meta-schema which defines the concept and structure of expressing geometric datatypes in XML. To accomplish this, the concept of a Geometry datatype needs to be expressible at the schema level.

Of course, for any given application domain you can dodge this issue by simply relying on convention. A datatype with more than trivial semantics is going to have a custom implementation in any given system, so a custom mapping from XML will be needed in any case. But that's not really the point - surely at this stage of computer science we can do better than arbitrary convention?

I haven't yet seen an explanation of whether RELAX-NG provides this level of expressiveness. I don't see it in JSON or YAML. But it seems like this capability is essential for any schema language which is going to take us beyond simply collections of a small set of datatypes.

RELAX NG good, XML Schema bad?

Here's a nice post on why RELAX NG is better than XML Schema. Since data modelling and language expressiveness are a major interest, I'm finding it fascinating to watch the evolutionary battles in the world of "meta-XML".

One key point made is that RNG is much easier to grasp than XML Schema. Witness this short tutorial which tells you most of what you need to know.

Something I haven't fully understood yet is why RNG fans consider PSVI to be a bad idea. As far as I see, any tool which is a general purpose parser for typed XML is going to have to define a metamodel describing the allowable range of documents. Doesn't it make sense to have a standard model for this?

Another thing I don't see is whether and how RNG supports the constrained extensibility of schemas (i.e. subclassing). This is responsible for a fair bit of the complexity in XML Schema, but is essential in some uses (such as GML, which is really a schema framework for defining other concrete schemas).

Probably the most appealing aspect of RNG is its compact syntax. It's much more readable than XML. (XML is a terrible syntax for expressing a hierarchical language!). Of course, this means the end of the "one parser to scan them all" dream - but perhaps that's a good thing. Come back, YACC, we really didn't mean it and we still love you!

This post gives a rebuttal to the RNG-over-XSD argument. He seems to think that RNG lacks subclassing as well, so maybe that answers one of my questions above.

Streaming Delaunay Triangulation for Huge Datasets

Isenburg, Liu, Shewchuk and Snoeyink have an interesting paper on contructing Delaunay triangulations over huge datasets using a streaming technique.


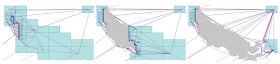
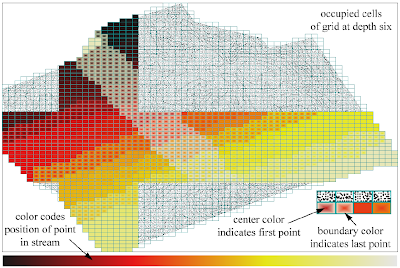
I'm quite interested in this, because here at Refractions I've just finished working on a project which involved computing a TIN for the province of B.C. using 500 million masspoints. After briefly flirting with the idea of computing a single seamless TIN, I ended up computing it in a piecewise fashion. This probably turned out to be a better approach for other reasons (such as the fact that we could easily parallelize the process). However, it would be very cool to be able to compute a seamless TIN for the entire province. And the approach in this paper sounds very effective - they quote a billion triangle in 48 minutes on a laptop!

It's also exciting to see the emergence of a whole new class of algorithms focussed on dealing with VLSD's (very large spatial datasets). As the same authors point out in another paper, paradoxically, advances in computing technology can make geospatial processing more difficult
because the rate of growth of dataset size far outstrips memory capacity.

Incidentally, these guys are a bit of a dream team for computational geometry algorithms. Shewchuck is the developer of Triangle, one of the best known programs for computing constrained 2D Delaunay triangulations (which is also AFAIK one of the few available systems to seriously address robustness issues - JTS of course being another one!) Snoeyink has done research in all kinds of different areas of CG, including interesting work in computing watershed boundaries on TINs using B.C. data.

The paper also has a nice way of showing the spatial distribution of two related variables, using fill gradients:

Slow Forward - or back?

Here's an interesting take on the technological revolution by Gwynne Dyer (contrarian as always!). His point is that while life was dramatically transformed by numerous new technologies introduced between the 18th century and the 1950s, since then there's only really been one transformative technology, the computer (I guess he's discounting space travel since it's not generally available, or maybe because it's irrelevant?).

He has a good point, but I wonder whether he's ignoring quantitative effects of change. Sure, planes were around in the early 20th century, but they weren't allowing huge numbers of people to wash around the world in the way they do now. 9/11 would have been impossible in the 1920's, for instance. And maybe the steady improvments in speed of communication really will result in the so-called "inflection point".

But... in the end, he does mention what may turn out to be the most important quantitative effect of technological developments on humanity. His final point talks about the coming "... drastic changes in the climate that affect everything ...".

Engines of Logic

It seems only right that I put in a plug for the book Engines of Logic by the other, more famous Martin Davis. And here's an interesting article which reviews the book in particular reference to the occupational health hazards of being a mathematician. It's a good antidote to any regrets you might have about not being real smart.

Quote of the Day

If it wasn't for Alan Turing, I'd either be unemployed or working for the Nazis.

- unknown IT worker

The Vietnam of Computer Science?

I couldn't resist the analogy of this blog article, even if the author slightly overstates the case. Good summary of the history of the war, too.

Makes me feel like if I haven't served a tour in the Delta, at least I've done time at a forward fire base...

Complex Functions as Algorithmic Art

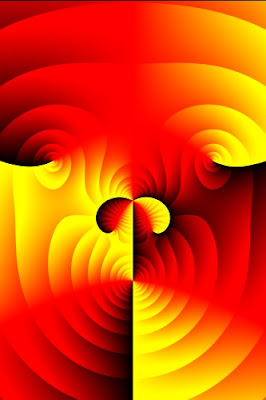
Hans Lundmark has an interesting page on visualizing complex functions. The idea is to map functions from f : C → C using position, hue, and saturation. The domain values of the function provide the (x, y) position. The function output value provides the hue and saturation; the hue is determined by the complex argument (angle), and the saturation is determined by the absolute value.

The output struck me as a nice example of algorithmic art. I whipped up my own version in Java to experiment, and to be able to produce high-resolution images for printing. Here's a couple of my images:

An example function from the paper ( f ( z ) = ( z − 2 )² ( z + 1 − 2i ) ( z + 2 + 2i ) / z³ )



^{"Wild Walrus"}

PreparedGeometry - efficient batch spatial operations for JTS

A common usage pattern for JTS spatial operations (in particular, predicates such as intersects and contains, and overlay operations such as intersection and union) involves the operation being invoked between a single target geometry and a batch of test geometries. For instance, this occurs in queries in a spatial database such as PostGIS, where each geometry in the driving table interacts with a set of nearby geometries via the required operation. By taking advantage of the fact that the target geometry does not change, it is possible to significantly reduce the overall execution cost of the operation. Information such as an index on the line segments in the target geometry can be computed once and cached for reuse with all of the test geometries.

In order for this to work, the calling code must be able to indicate that the operation is being invoked in a batch setting. The standard JTS Geometry API doesn't allow differentiating this case, so the new concept of PreparedGeometry has been developed. (This name intentionally echoes the concept of prepared statement in SQL API's, which implements the same strategy.) Creating a PreparedGeometry on a target Geometry enables precomputation of various data structures, which then allows subsequent operations to be evaluated with maximum efficiency.

In addition to caching, it is also possible to optimize the evaluation of spatial predicates. Optimization takes the form of short-circuiting predicate evaluation when certain situations are detected. While not all OGC spatial predicates are amenable to optimization, fortunately the most commonly usd predicates, intersects and contains, can be optimized significantly. Examples of situations which can be optimized are:

• For intersects, any intersection between line segments indicates a true result. If there is no intersection between any line segments of the operands, and the target geometry is polygonal, then one or more fast point-in-polygon tests can be performed to compute the result value.
• Since it provides more information than intersects, the contains predicate is more complex to optimize. In the case where the target geometry is polygonal, evaluation can be short-circuited when the test geometry has no line segment intersection. In this case, containment can be tested by an appropriate set of point-in-polygon tests. It is also possible to short-circuit in some specific cases where a proper intersection is detected between two line segments. Both of these situations can be tested efficiently.

The performance gains from using PreparedGeometry in real-world situations can be dramatic - up to 40 times improvement in speed. This functionality will appear in the next release of JTS, and hopefully will make its way into GEOS and PostGIS as well.