- Iterated Union: Iterate over the polygons and union them one-by-one into a result polygon
- Buffer Union: Collect the polygons into a GeometryCollection and run buffer(0) on the collection
Since this is such a common operation, I've been keen to find a faster and more robust approach. An alternative strategy is to use a concept I call Cascaded Union. The idea is to union small subsets of the input together, then union groups of the resulting polygons, and so on recursively until the final union of all areas is computed. This can be thought of as a post-order traversal of a tree, where the union is performed at each interior node. If the tree structure is determined by the spatial proximity of the input polygons, and there is overlap or adjacency in the input dataset, this algorithm can be quite efficient. This is because union operations higher in the tree are faster, since linework is "merged away" from the lower levels.
This picture shows the algorithm in action:
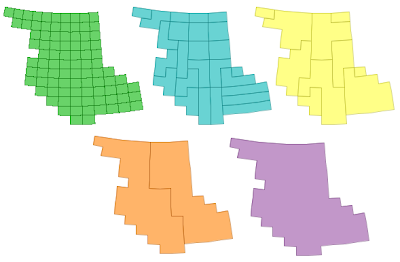
Handily, the spatial indexes already in JTS can be used to determine an appropriate tree structure. Currently the Sort-Tile-Recursive packed R-Tree index is used - this seems to produce an effective tree (although I suspect that the algorithm is not very senstive to the precise spatial tree used)
It turns out that Cascaded Union can be much more efficient than Iterated Union. On a test dataset with 30,000 small polygons with a high degree of overlap, the performance results were:
Cascaded Union: 20 sec
Iterated Union: 3 hours 40 min !
Not bad - well worth the effort of coding... Also, it's more robust than Buffer Union, and often much faster as well.
This will be provided via the Geometry.union() (Unary union) method in JTS 1.9.







12 comments:
I'm coming to this a little late - about a month after it was posted -- but I just recently discovered your blog. I was having robustness problems with buffer(0) in the upcoming release of My World GIS, and I happened upon a pretty similar solution. It didn't occur to me to use a spatial index, though; I just use a linked list and repeatedly pull the first two elements from the front of the list and put their union at the end of the list:
(unfortunately, the <code> tag is not allowed in comments so this may look a bit messy):
public Geometry computeUnion (Geometry geom)
{
if (geom instanceof GeometryCollection)
{
GeometryCollection collection = (GeometryCollection)geom;
LinkedList glist = new LinkedList();
for (int i = 0; i < collection.getNumGeometries(); i += 1)
{
glist.add(computeUnion(collection.getGeometryN(i)));
}
while (glist.size() > 1)
{
Geometry geom1 = (Geometry)glist.removeFirst();
Geometry geom2 = (Geometry)glist.removeFirst();
Geometry result = geom1.union(geom2);
if (result.getClass() == GeometryCollection.class)
{
glist.addLast(collapse((GeometryCollection)result));
}
else
{
glist.addLast(result);
}
}
return (Geometry)glist.getFirst();
}
else
{
return geom;
}
}
(the collapse method takes the collection and turns it into a MultiPolygon)
I'm really looking forward to JTS 1.9 now, as I'm sure using the spatial index makes the behavior of the union method more predictable.
Yep, indexing is key to making union efficient. Iterated union (what you've implemented) can be *very* slow in some cases. Using an index can speed this up dramatically (by eliminating lots of segments which don't appear in the final result).
Hello, I'm working in polygons union considering the including of holes in to them (a ring by example ...), but my problem doesn't have a real espacial order for indexing. Did you work with this type of polygons??
Yes, this algorithm handles polygons with holes no problem, since it uses the standard JTS union() method for actually merging pairs of polygons. JTS provides full support for polygons with holes.
Hi professor, in my problem the polygons also have internal segments and points as degenerated holes. So, there are several cases of interaction between borders. If this problem is fixed by the framework, I would like to use it. How can I get it?
Hi professor, in my problem the polygons also have internal segments and points as degenerated holes. So, there are several cases of interaction between borders. If this problem is fixed by the framework, I would like to use it. How can I get it?
Necho,
I'm not entirely sure what you mean. If the input polygons are valid (according to JTS) then the Cascaded Union should complete successfully. If the polygons are not valid, then you have to clean them up - which all depends on how they are invalid.
For more assistance you should post a description of the problem and sample data to the JTS user list.
Has this "Cascaded Union" been rolled into JTS 1.9? The union operation I am calling (multigeometryInstance.union()) appears to result in a simplified geometry. For example, I have loaded a bunch of multipolygons (county subdivisions from the US Census for the state of PA) added them all to a multigeometry and called union on the multigeometry. The resulting geometry's border appears to be smoother than it was when I rendered all the multiplogons individually.
Yes, CascadedUnion is in JTS 1.9, and is invoked by the Geometry.union() method.
Best thing to do would be to post some samples of your problem on the JTS list.
this is great, this reduced my program from 25 minutes to 1 minute!
Good to hear, Tommy - thanks.
Post a Comment