RelateNG Performance

A previous post introduced a new algorithm in the JTS Topology Suite called RelateNG.  It computes topological relationships between geometries using the Dimensionally-Extended 9 Intersection Model  (DE-9IM) model.  

This algorithm is fundamental to a large proportion of spatial queries executed in numerous geospatial environments.  It would not be surprising to learn that the Relate algorithm is executed billions of times per day across the world's data centres.  Given this, performance is a critical metric.  

The original JTS RelateOp algorithm was hamstrung by its design, which required computing a full topology graph for each relationship evaluation.  The subsequent development of PreparedGeometry provided a significant performance boost for common spatial predicates such as intersects and covers.  A useful side-effect is that it is less susceptible to geometric robustness problems.  However, it has some drawbacks:

• it only implements a small set of predicates
• the design does not easily extend to more complex predicates
• it does not support GeometryCollection inputs
• it is a completely separate codebase to the general-purpose RelateOp, which increases maintenance effort and increases the risk of bugs and behaviour discrepancies

RelateNG solves all of these problems.  In addition, it provides much better performance for non-prepared (stateless) calls.  This is important for systems which do not execute spatial queries in a stateful way (due to architectural limitations, or simply lack of attention to performance), and thus cannot use prepared mode.

Performance Tests

Here are some examples of performance metrics.  

Note that the data used in the tests is sometimes subsetted to avoid skewing the results with many false results due to non-interaction between the input geometries.  This reflects the typical deployment of these predicates in systems which perform a primary extent filter (i.e. via a spatial index) before executing the full predicate.

Some of datasets are in geodetic coordinates, which strictly speaking JTS does not handle. But this does not matter for the purposes of performance testing.

Point / Polygon

This test queries a MultiPolygon of the outline of Europe (including larger islands) against a synthetic dataset of random points.  The test evaluates the intersects predicate, which is really the only one of interest in the Point / Polygon case.  

The test data metrics are:

• Query MultiPolygon: 461 polygons, 22,675 vertices
• Target Points: 10,000 points

Timings

Op	Intersects	Intersects Prep
Relate	61.7 s	21 ms
RelateNG	0.1 s	19 ms

The result clearly shows the enormous improvement in the stateless case, since RelateNG does not build topology on the input polygon.  The results are very similar in the prepared case.  This is as expected, since both codebases run a simple Point-in-Polygon test using a cached spatial index.

Line / Line

This test uses a dataset of major rivers of the continental United States.  A single river mainstem is queried against a subset of river branches using the intersects and touches relationships, in stateless and prepared modes.

The test data metrics are:

• Query Line: 6,975 vertices
• Target Lines: 407 lines with 47,328 vertices

 

Timings (per 100 executions of the operation)

Op	Intersects	Intersects Prep	Touches	Touches Prep
Relate	38.2 s	133 ms	36 s	N/A
RelateNG	1.18 s	142 ms	2.05 s	2.03 s

This shows the much better performance of RelateNG.  RelateNG can evaluate touches in prepared mode, but the performance is similar to stateless mode, since currently indexes are not cached for Line/Line cases.  This could be improved in a future release.

Polygon / Polygon

This test uses data from two polygonal datasets:

• The Britsh Columbia Bedrock Geology polygonal coverage
• The GADM Level 2 boundaries for Canada

The tests query an administrative unit polygon against a subset of Bedrock polygons which intersect its extent, using intersects and covers in stateless and prepared modes. 

The test data metrics are:

• GADM unit: 4,017 vertices
• Bedrock polygons: 4,318 polygon with 337,650 vertices

Timings (per 100 executions of the operation)

Op	Intersects	Intersects Prep	Covers	Covers Prep
Relate	61.7 s	534 ms	54.9 s	842 ms
RelateNG	5.8 s	595 ms	6.4 s	943 ms

Polygon / Polygon - Custom Relate Pattern

The tests shows the ability of RelateNG to efficiently evaluate arbitrary Relate Intersection Matrix patterns.  In this case, the pattern used is F***0****, which corresponds to a relationship which could be called "point-touches": two geometries have boundaries which intersect in only one (or more) points (dimension 0), but whose interiors do not intersect.

This test uses data from The GADM Level 1 boundaries for Canada.  This has the advantage that Canada contains a rare example of 4 boundaries meeting at a single point (the jurisdictions of Saskatchewan, Manitoba, Northwest Territories, and Nunavut).

The test data metrics are:

• GADM Canada Level 1: 13 polygons, 4,005,926 vertices

Timings

Op	F***0****	F***0**** Prep
Relate	504 s	N/A
RelateNG	9.8 s	6.6 s

As expected, for this test RelateNG is far more performant than Relate.  This is due to its ability to analyze Intersection Matrix patterns and perform only topology tests that are necessary, as well as not building a full topological structure of the inputs.  The test shows the effect of caching spatial indexes in prepared mode, although stateless mode is very efficient as well.

Analysis of Results

Clearly RelateNG is far more performant than Relate when running in non-prepared mode.  The PreparedGeometry implementation is slightly faster (which confirms the efficiency of its original design), but not by very much.  The difference may be a consequence of the general-purpose and thus more complex code and data structures in RelateNG. Closing this gap may be an area for future research.

One thing is certain: the RelateNG algorithm design provides much more scope for adding case-specific optimizations.  If you have a significant use case which could be improved by further targeted optimization improvements, let me know in the comments!

It will be interesting to re-evaluate these tests once RelateNG is ported to GEOS.  Sometimes (but not always) a C++ implementation can be significantly faster than Java, due to more opportunities for code and compiler optimization.

JTS Topological Relationships - the Next Generation

The most fundamental and widely-used operations in the JTS Topology Suite are the ones that evaluate topological relationships between geometries.  JTS implements the Dimensionally-Extended 9 Intersection Model (DE-9IM), as defined in the OGC Simple Features specification, in the RelateOp API.  

DE-9IM matrix for overlapping polygons

The RelateOp algorithm was the very first one implemented during the initial JTS development, over 20 years ago.  At that time it was an appealing idea to implement a general-purpose topology framework (the GeometryGraph package), and use it to support topological predicates, overlay, and buffering.  However, some disadvantages of this approach have become evident over time:

• the need to create a topological graph structure limits the ability to improve performance. This has led to the implementation of PreparedGeometry - but that adds further complexity to the codebase, and supports only a limited set of predicates.
• a large number of code dependencies make it hard to fix problems and improve semantics
• constructing a full topology graph increases exposure to geometric robustness errors
• GeometryCollections are not supported (initially because the OGC did not define the semantics for this, and now because adding this capability is difficult)

There's an extensive list of issues relating (ha!) to RelateOp here.

The importance of this functionality is especially significant since the same algorithm is implemented in GEOS.  That codebase is used to evaluate spatial queries in popular spatial APIs such as Shapely and R-sf, and numerous systems such as PostGIS, DuckDB, SpatialLite, QGIS, and GDAL (to name just a few).  It would not be surprising to learn that the RelateOp algorithm is executed billions of times per day across the world's CPUs.

During the subsequent years of working on JTS I realized that there was a better way to evaluate topological relationships.  It would required a ground-up rewrite, but would avoid the shortcomings of RelateOp and provide better performance and a more tractable codebase.  Thanks to my employer Crunchy Data I have finally been able to make this idea a reality.  Soon JTS will provide a new algorithm for topological relationships called RelateNG.

Key Features of RelateNG

The RelateNG algorithm incorporates a broad spectrum of improvements over RelateOp in the areas of functionality, robustness, and performance.  It provides the following features:

• Efficient short-circuited evaluation of topological predicates (including matching custom DE-9IM matrix patterns)
• Optimized repeated evaluation of predicates against a single geometry via cached spatial indexes (AKA "prepared mode")
• Robust computation (only point-local geometry topology is computed, so invalid topology does not cause failures)
• GeometryCollection inputs containing mixed types and overlapping polygons are supported, using union semantics.
• Zero-length LineStrings are treated as being topologically identical to Points.
• Support for BoundaryNodeRules.

Using the RelateNG API

The main entry point is the RelateNG class.  It supports evaluating topological relationships in three different ways:

• Evaluating a standard OGC named boolean binary predicate, specified via a TopologyPredicate instance.  Standard predicates are obtained from the RelatePredicate factory functions intersects, contains, overlaps, etc.
• Testing an arbitrary DE-9IM relationship by matching an intersection matrix pattern (e.g. "T**FF*FF*", which is the pattern for a relation called Contains Properly).
• Computing the full value of a DE-9IM IntersectionMatrix.

RelateNG operations can be executed in two modes: stateless and prepared.  Stateless mode is provided by the relate static functions, which accept two input geometries and evaluate a predicate.  For prepared mode, a single geometry is provided to the prepare functions to create a RelateNG instance.  Then the evaluate instance methods can be used to evaluate spatial predicates on a sequence of geometries. The instance creates spatial indexes (lazily) to make topology evaluation much more efficient.  Note that even stateless mode can be significantly faster than the current implementation, due to short-circuiting and other internal heuristics.

Here is an example of matching an intersection matrix pattern, in stateless mode:

boolean isMatched = RelateNG.relate(geomA, geomB, "T**FF*FF*");

Here is an example of setting up a geometry in prepared mode, and evaluating a named predicate on it:

RelateNG rng = RelateNG.prepare(geomA);
for (Geometry geomB : geomSet) {
    boolean predValue = rng.evaluate(geomB, RelatePredicate.intersects());
}

Rolling It Out

It's exciting to launch a major improvement on such a core piece of spatial functionality.  The Crunchy spatial team will get busy on porting this algorithm to GEOS.  From there it should get extensive usage in downstream projects.  We're looking forward to hearing feedback from our own PostGIS clients as well as other users.  We're always happy to be able to reduce query times and equally importantly, carbon footprints.  

In further blog posts I'll describe the RelateNG algorithm design and provide some examples of performance metrics.

Future Ideas

The RelateNG implementation provides an excellent foundation to build out some interesting extensions to the fundamental DE-9IM concept.

Extended Patterns

The current DE-9IM pattern language is quite limited.  In fact, it's not even powerful enough to express the standard named predicates.  It could be improved by adding features like:

• disjunctive combinations of patterns.  For example, touches is defined by  "FT******* | F**T***** | F***T****"
• dimension guards to specify which dimensions a pattern applies to.  For example, overlaps is defined by "[0,2] T*T***T** | [1] 1*T***T**"
• while we're at it, might as well support dotted notation and spaces for readability; e.g. "FT*.***.***"

Approximate Spatial Relationships

A requirement that comes up occasionally is to compute approximate spatial relationships between imprecise data using a distance tolerance.  This is useful in datasets where features don't match exactly due to data inaccuracy. Because RelateNG creates topology only in the neighbourhood of specified points, it should be possible to specify the neighbourhood size using a distance tolerance.  Essentially, vertices and line intersections will "snap together" to determine the effective topology.  Currently within-distance queries are often used to compute "approximate intersects".  Adding a distance tolerance capability to RelateNG will allow other kinds of approximate relationships to be evaluated as well.

Further Performance Optimizations?

A challenge with implementing algorithms over a wide variety of spatial types and use cases is how to provide general-purpose code which matches (or exceeds) the efficiency of more targeted implementations.  RelateNG analyzes the input geometries and the predicate under evaluation to tune strategies to reduce the amount of work needed to evaluate the DE-9IM.  It may be that profiling specific use cases reveals further hotspots in the code which can be improved by additional optimizations.  

Curve Support

GEOS has recently added support for representing geometries with curves.  The RelateNG design is modular enough that it should be possible to extend it to allow evaluating relationships for geometries with curves.  

Simplifying Polygonal Coverages with JTS

A new capability for the JTS Topology Suite is operations to process Simple Polygonal Coverages.  A Simple Polygon Coverage is a set of edge-matched, non-overlapping polygonal geometries (which may be non-contiguous, and have holes).  Typically this is used to model an area in which every point has a value from some domain.  A classic example of a polygonal coverage is a set of administrative boundaries, such as those available from GADM or Natural Earth.

GADM polygonal coverage for France Level 1   ( 198,350 vertices)

The first coverage operations provided are:

• Coverage Validation, to check if a set of polygons forms a topologically-valid coverage
• Coverage Union, which takes advantage of coverage topology to provide a very fast union operation

Another operation on polygonal coverages is simplification.  Simplifying a coverage reduces the number of vertices it contains, while preserving the coverage topology.  Preserving topology means that the simplified polygons still form a valid coverage, and that polygons which had a common edge in the input coverage (i.e. which were adjacent) still share an edge in the simplified result.  Reducing dataset size via simplification can provide more efficient storage and download, and faster visualization at smaller scales.

France coverage simplified with tolerance 0.01   (7,918 vertices)

The decrease in resolution is hardly noticeable at this scale

Closeup of simplified coverage (tolerance = 0.01)

Simplification is perhaps the most requested algorithm for polygonal coverages (for example, see GIS StackExchange questions here, here and here.)  My colleague Paul Ramsey sometimes calls it the "killer app" for polygonal coverages.  Earlier this century there was no easily-available software implementing this capability.  Users often had to resort to the complex approach of extracting the linework from the dataset, dissolving it, simplifying the lines (with a tool which would not cause further overlaps), re-polygonizing, and re-attaching feature attribution to the result geometries. 

More recently tooling has emerged to provide this functionality.  Simplification is the raison-d'etre of the widely-used and cited MapShaper tool.  GRASS has the v.generalize module.  And good old OpenJUMP added Simplify Polygon Coverage a while back.  

JTS has provided the TopologyPreservingSimplifier algorithm for many years, but this only operates on Polygons and MultiPolygons, not on polygonal coverages.  (Attempting to use it on polygonal coverages can introduce gaps and overlaps, resulting in complaints like this.)  But coverage simplification has been lacking in JTS/GEOS - until now.

JTS Coverage Simplification

Recent work on Polygon Hulls provided ideas for an implementation of coverage simplification. The CoverageSimplifier class uses an area-based simplification approach similar to the well-known Visvalingam-Whyatt algorithm. This provides good results for simplifying areal features (as opposed to linear ones).  It's possible to use a Douglas-Peucker based approach as well, so this may be a future option.

The degree of simplification is determined by a tolerance value.  The value is equivalent roughly to the maximum distance a simplified edge can change (technically speaking, it is the square root of the area tolerance for the Visvalingam-Whyatt algorithm).  

The algorithm progressively simplifies all coverage edges, while ensuring that no edges cross another edge, or touch at endpoints.  This provides the maximum amount of simplification (up to the tolerance) while still maintaining the coverage topology.

The coverage of course should be valid according to the JTS CoverageValidator class.  Invalid coverages can still be simplified, but only edges with valid topology will have it maintained.

France coverage simplified with tolerance = 0.1   ( 1,928 vertices)

France coverage simplified with tolerance = 0.5    ( 1,527 vertices)

The coverage topology (adjacency relationship) is always preserved.

Inner Simplification

The implementation also provides the interesting option of Inner Simplification.  This mode simplifies only inner, shared edges, leaving the outer boundary edges unchanged.  This allows portions of a coverage to be simplified, by ensuring that the simplified polygons will fit exactly into the original coverage.  (This GIS-SE question is an example of how this can be used.)

Inner Simplification of France coverage

It would also be possible to provide Outer Simplification, where only outer edges are simplified.  It's not clear what the use case would be for this - if you have ideas, leave a comment!

GEOS and PostGIS

As usual, this algorithm will be ported to GEOS, from where it will be available to downstream projects such as PostGIS and Shapely.  

For PostGIS, the intention is to expose this as a window function (perhaps ST_CoverageSimplify).  That will make it easy to process a set of features (records) and maintain the attributes for each feature.

Fast Coverage Union in JTS

The next operation delivered in the build-out of Simple Polygonal Coverages in the JTS Topology Suite is Coverage Union. This is simply the topological union of a set of polygons in a polygonal coverage, producing one or more polygons as the result.  (This is sometimes called "dissolve" in the context of polygonal coverages.)

Union of polygons has long been available in JTS, most recently (and robustly) as the UnaryUnion capability of OverlayNG.  This makes use of the Cascaded Union technique to provide good performance for large sets of polygons.  But the constrained structure of polygonal coverages means unions can be computed much faster than even Cascaded Union.  Essentially, the duplicated inner edges of adjacent polygons are identified and discarded, leaving only the outer boundary of the unioned area.  Because a valid polygonal coverage has edges which match exactly, identifying duplicate segments can be done with a fast equality test.  Also, there is no need for computationally-expensive techniques to ensure geometric robustness.

This is now available in JTS as the CoverageUnion class.

Performance

To test the performance of Coverage Union we need some large clean polygonal coverages. These are nicely provided by the GADM repository of worldwide administrative areas.  

Here is some metrics comparing the performance of Coverage Union against OverlayNG Unary Union (which uses the Cascaded Union technique).  Coverage Union is much faster for all sizes of dataset.

Dataset	Polygons	Vertices	Coverage Union	OverlayNG Union	Times Faster
France level 4	3,728	407,102	0.3 s	8.5 s	28 x
France level 5	36,612	729,573	1.07 s	13.9 s	13 x
Germany level 4	11,302	2,162,184	0.68 s	27.3 s	40 x

Union by Attribute

It's worth noting that unioning a set of polygons in a coverage leaves the boundary of the unioned area perfectly unchanged. So subsets of a coverage can be unioned, and the result still forms a valid polygonal coverage.  This provides a fast Union by Attribute capability, which is a common spatial requirement. 

GEOS and PostGIS

GEOS already supports a GEOSCoverageUnion operation.  At some point it would be nice to expose this in PostGIS, most likely as a new aggregate function (perhaps ST_UnionCoverage).

Alpha Shapes in JTS

Recently JTS gained the ability to compute Concave Hulls of point sets.  The algorithm used is based the Chi-shapes approach described by Duckham et al.   It works by eroding border triangles from the Delaunay Triangulation of the input points, in order of longest triangle edge length, down to a threshold length provided as a parameter value.  

Concave Hull of Ukraine (Edge-length = 10)

Alpha-Shapes

Another popular approach for computing concave hulls is the Alpha-shape construction originally proposed by Edelsbrunner et al.  Papers describing alpha-shapes tend to be lengthy and somewhat opaque theoretical expositions, but the actual algorithm is fairly simple.  It is also based on eroding Delaunay triangles, but uses the circumradius of the triangles as the criteria for removal.  Border triangles whose circumradius is greater than alpha are removed.  

Another way of understanding this is to imagine triangles on the border of the triangulation being "scooped out" by a disc of radius alpha:

Construction of an Alpha-shape via "scooping" with an alpha-radius disc

Given the similar basis of both algorithms, it was easy to generalize the JTS ConcaveHull class to be able to compute alpha-shapes as well.  This is now available in JTS via the ConcaveHull.alphaShape function.

Seeking Alpha

An issue that became apparent was: what is the definition of alpha?  There are at least three alternatives in use:

• The original Edelsbrunner 1983 paper defines alpha as the inverse of the radius of the eroding disc.
• In a later 1994 paper Edelsbrunner defines alpha as the radius of the eroding disc.  The same definition is used in his 2010 survey of alpha shape research.
• The CGAL geometry library implements alpha to be the square of the radius of the eroding disc.  (The derivation of this definition is not obvious to me; perhaps it is intended to make the parameter have areal units?)

The simplest option is to define alpha to be the radius of the eroding disc.  This has the additional benefit of being congruent with the edge-length parameter.  For both parameters, 0 produces a result with maximum concaveness, and for values larger than some (data-dependent) value the result is the convex hull of the input.

Alpha-Shape VS Concave Hull

An obvious question is: how do alpha-shapes differ to edge-length-based concave hulls?  Having both in JTS makes it easy to compare the hulls on various datasets.  For comparison purposes the alpha and edge-length parameters are chosen to produce hulls with the same area (as close as possible).

Here's an illustration of an Alpha-shape and a Concave Hull generated for the same dataset, with essentially identical area.

Overall the shapes are fairly similar.  Alpha-shapes tend to follow the data points more closely in "shallow bays", whereas the concave hull tends to include them.  Conversely, the concave hull can sometimes erode deeper bays.  The effect of keeping shallow bays is to make the Concave Hull slightly smoother than the Alpha-shape.

Avoiding Cavities

However, there is one way in which alpha-shapes can be less well-formed than concave hulls.  The measurement of a circumradius is independent of the orientation of the triangle.  This means it is not sensitive to whether the triangle has a long or short edge on the border of the triangulation.  This can result in what I am calling "cavitation". Cavitation occurs where narrow triangles reaching deep into the interior of the dataset are removed. This in turn exposes more interior triangles to being eroded.  This is visible in the example below, where the Alpha-shape contains a large cavity which is obviously not desirable. 

Alpha-shape with a "cavity"

This is shown in more detail below.  The highlighted triangle is removed due to its large circumradius, even though it has a relatively small border edge.  This in turn exposes more triangles to being removed, forming the undesirable cavity.

Alpha-shape with Delaunay triangle forming a "cavity"

The edge-length metric does not have this problem, since it considers only the edges along the (current) border of the triangulation.  (In fact, the presence of the cavity in the example above means that the equal-area comparison strategy causes more erosion artifacts in the Concave Hull than might otherwise be present.)

For an even more egregious example of this issue, here is an Alpha-shape of the Ukraine dataset:

Alpha-shape of Ukraine (alpha = 7)

The effect of cavitation is obvious.  Although it can be eliminated by increasing the alpha radius, note that Crimean Peninsula is already less well-delineated than in the Concave Hull, and increasing alpha would make this worse. 

Recommendation

Given the risk of undesired cavitation, the safest option for computing Concave Hulls is to use the Edge-Length approach, rather than Alpha-shapes.   

Future Work

• Best of Both? - perhaps there is a strategy which combines aspects of both Alpha-shapes and Concave Hulls, to erode shallow bays but avoid the phenomenon of cavitation?
• Disconnected Hulls - the "classic" Alpha-shape definition allows disconnected MultiPolygons as a result.  Currently, the JTS algorithm always produces a result which is a connected single polygon.  This seems like the most commonly desired behaviour, but there is a possibility to extend the implementation to optionally allow a disconnected result .  CGAL provides a parameter to control the number of polygons in the result, which could be implemented as well.

Relational Properties of DE-9IM spatial predicates

There is an elegant mathematical theory of binary relations.  Homogeneous relations are an important subclass of binary relations in which both domains are the same.  A homogeneous relation R is a subset of all ordered pairs (x,y) with x and y elements of the domain.  This can be thought of as a boolean-valued function R(x,y), which is true if the pair has the relationship and false if not.

The restricted structure of homogeneous relations allows describing them by various properties, including:

Reflexive - R(x, x) is always true

Irreflexive - R(x, x) is never true

Symmetric - if R(x, y), then R(y, x)

Antisymmetric - if R(x, y) and R(y, x), then x = y

Transitive - if R(x, y) and R(y, z), then R(x, z)

The Dimensionally Extended 9-Intersection Model (DE-9IM) represents the topological relationship between two geometries.  

Various useful subsets of spatial relationships are specified by named spatial predicates.  These are the basis for spatial querying in many spatial systems including the JTS Topology Suite, GEOS and PostGIS.

The spatial predicates are homogeneous binary relations over the Geometry domain  They can thus be categorized in terms of the relational properties above.  The following table shows the properties of the standard predicates:

Predicate	Reflexive / Irreflexive	Symmetric / Antisymmetric	Transitive
Equals	R	S	T
Intersects	R	S	-
Disjoint	R	S	-
Contains	R	A	-
Within	R	A	-
Covers	R	A	T
CoveredBy	R	A	T
Crosses	I	S	-
Overlaps	I	S	-
Touches	I	S	-

Notes

• Contains and Within are not Transitive because of the quirk that "Polygons do not contain their Boundary" (explained in this post).  A counterexample is a Polygon that contains a LineString lying in its boundary and interior, with the LineString containing a Point that lies in the Polygon boundary.  The Polygon does not contain the Point.  So Contains(poly, line) = true and Contains(line, pt) = true, but Contains(poly, pt) = false.   The predicates Covers and CoveredBy do not have this idiosyncrasy, and thus are transitive.

Validating Polygonal Coverages in JTS

The previous post discussed polygonal coverages and outlined the plan to support them in the JTS Topology Suite.  This post presents the first step of the plan: algorithms to validate polygonal coverages.  This capability is essential, since coverage algorithms rely on valid input to provide correct results.  And as will be seen below, coverage validity is usually not obvious, and cannot be taken for granted.  

As described previously, a polygonal coverage is a set of polygons which fulfils a specific set of geometric conditions.  Specifically, a set of polygons is coverage-valid if and only if it satisfies the following conditions:

• Non-Overlapping - polygon interiors do not intersect
• Edge-Matched (also called Vector-Clean and Fully-Noded) - the shared boundaries of adjacent polygons has the same set of vertices in both polygons

The Non-Overlapping condition ensures that no point is covered by more than one polygon.  The Edge-Matched condition ensures that coverage topology is stable under transformations such as reprojection, simplification and precision reduction (since even if vertices are coincident with a line segment in the original dataset, this is very unlikely to be the case when the data is transformed).  

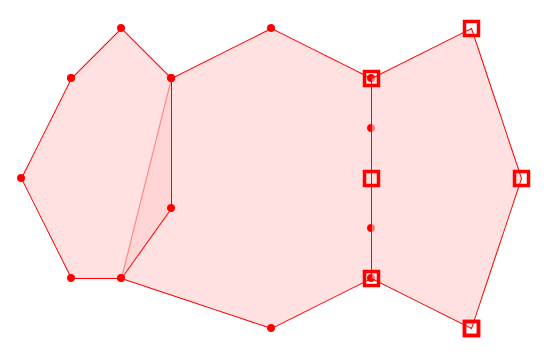
An invalid coverage which violates both (L) Non-Overlapping and (R) Edge-Matched conditions (note the different vertices in the shared boundary of the right-hand pair)

Note that these rules allow a polygonal coverage to cover disjoint areas.  They also allow internal gaps to occur between polygons.  Gaps may be intentional holes, or unwanted narrow gaps caused by mismatched boundaries of otherwise adjacent polygons.  The difference is purely one of size.  In the same way, unwanted narrow "gores" may occur in valid coverages.  Detecting undesirable gaps and gores will be discussed further in a subsequent post. 

Computing Coverage Validation

Coverage validity is a global property of a set of polygons, but it can be evaluated in a local and piecewise fashion.  To confirm a coverage is valid, it is sufficient to check every polygon against each adjacent (intersecting) polygon to determine if any of the following invalid situations occur:

• Interiors Overlap:
• the polygon linework crosses the boundary of the adjacent polygon
• a polygon vertex lies within the adjacent polygon
• the polygon is a duplicate of the adjacent polygon
• Edges do not Match:
• two segments in the boundaries of the polygons intersect and are collinear, but are not equal 

If neither of these situations are present, then the target polygon is coverage-valid with respect to the adjacent polygon.  If all polygons are coverage-valid against every adjacent polygon then the coverage as a whole is valid.

For a given polygon it is more efficient to check all adjacent polygons together, since this allows faster checking of valid polygon boundary segments.  When validation is used on datasets which are already clean, or mostly so, this improves the overall performance of the algorithm.  

Evaluating coverage validity in a piecewise way allows the validation process to be parallelized easily, and executed incrementally if required.

JTS Coverage Validation

Validation of a single coverage polygon is provided by the JTS CoveragePolygonValidator class.  If a polygon is coverage-invalid due to one or more of the above situations, the class computes the portion(s) of the polygon boundary which cause the failure(s).  This allows the locations and number of invalidities to be determined and visualized.

The class CoverageValidator computes coverage-validity for an entire set of polygons.  It reports the invalid locations for all polygons which are not coverage-valid (if any). 

Using spatial indexing makes checking coverage validity quite performant.  For example, a coverage containing 91,384 polygons with 10,474,336 vertices took only 6.4 seconds to validate.  In this case the coverage is nearly valid, since only one invalid polygon was found. The invalid boundary linework returned by CoverageValidator allows easily visualizing the location of the issue.

A polygonal dataset of 91,384 polygons, containing a single coverage-invalid polygon

The invalid polygon is a tiny sliver, with a single vertex lying a very small distance inside an adjacent polygon.  The discrepancy is only visible using the JTS TestBuilder Reveal Topology mode.

The size of the discrepancy is very small.  The vertex causing the overlap is only 0.0000000001 units away from being valid:

[921]  POLYGON(632)

[922:4]  POLYGON(5)

Ring-CW  Vert[921:0 514]  POINT ( 960703.3910000008 884733.1892000008 )

Ring-CW  Vert[922:4:0 3]  POINT ( 960703.3910000008 884733.1893000007 )

This illustrates the importance of having fast, robust automated validity checking for polygonal coverages, and providing information about the exact location of errors.

Real-world testing

With coverage validation now available in JTS, it's interesting to apply it to publicly available datasets which (should) have coverage topology.  It is surprising how many contain validity errors.  Here are a few examples:

Source	City of Vancouver
Dataset	Zoning Districts

This dataset contains 1,498 polygons with 57,632 vertices. There are 379 errors identified, which mainly consist of very small discrepancies between vertices of adjacent polygons.

Example of a discrepant vertex in a polygon

Source	British Ordnance Survey OpenData
Dataset	Boundary-Line
File	unitary_electoral_division_region.shp

This dataset contains 1,178 polygons with 2,174,787 vertices. There are 51 errors identified, which mainly consist of slight discrepancies between vertices of adjacent polygons. (Note that this does not include gaps, which are not detected by CoverageValidator.  There are about 100 gaps in the dataset as well.)

An example of overlapping polygons in the Electoral Division dataset

Source	Hamburg Open Data Platform
Dataset	VerwaltungsEinheit (Administrative Units)

The dataset (slightly reduced) contains 7 polygons with 18,254 vertices.  Coverage validation produces 64 error locations.  The errors are generally small vertex discrepancies producing overlaps.  Gaps exist as well, but are not detected by the default CoverageValidator usage.

An example of overlapping polygons (and a gap) in the VerwaltungsEinheit dataset

As always, this code will be ported to GEOS.  A further goal is to provide this capability in PostGIS, since there are likely many datasets which could benefit from this checking.  The piecewise implementation of the algorithm should mesh well with the nature of SQL query execution.

And of course the next logical step is to provide the ability to fix errors detected by coverage validation.   This is a research project for the near term.

UPDATE: my colleague Paul Ramsey pointed out that he has already ported this code to GEOS.  Now for some performance testing!

Polygonal Coverages and Operations in JTS

An important concept in spatial data modelling is that of a coverage.  A coverage models a two-dimensional region in which every point has a value out of a range (which may be defined over one or a set of attributes).  Coverages can be represented in both of the main physical spatial data models: raster and vector.  In the raster data model a coverage is represented by a grid of cells with varying values.  In the vector data model a coverage is a set of non-overlapping polygons (which usually, but not always, cover a contiguous area).  

This post is about the vector data coverage model, which is termed (naturally) a polygonal coverage. These are used to model regions which are occupied by discrete sub-regions with varying sets of attribute values.  The sub-regions are modelled by simple polygons.  The coverage may contain gaps between polygons, and may cover multiple disjoint areas.  The essential characteristics are:

• polygon interiors do not overlap
• the common boundary of adjacent polygons has the same set of vertices in both polygons.

There are many types of data which are naturally modelled by polygonal coverages.  Classic examples include:

• Man-made boundaries
• parcel fabrics
• political jurisdictions
• Natural boundaries
• vegetation cover
• land use

A polygonal coverage of regions of France

Topological and Discrete Polygonal Coverages

There are two ways to represent polygonal coverages: as a topological data structure, or as a set of discrete polygons.  

A coverage topology consists of linked faces, edges and nodes. The edges between two nodes form the shared boundary between two faces.  The coverage polygons can be reconstituted from the edges delimiting each face.  

The discrete polygon representation is simpler, and aligns better with the OGC Simple Features model.  It is simply a collection of polygons which satisfy the coverage validity criteria given above.

Most common spatial data formats support only a discrete polygon model, and many coverage datasets are provided in this form.  However, the lack of inherent topology means that datasets must be carefully constructed to ensure they have valid coverage topology.  In fact, many available datasets contain coverage invalidities.  A current focus of JTS development is to provide algorithms to detect this situation and provide the locations where the polygons fail to form a valid coverage.

Polygonal Coverage Operations

Operations which can be performed on polygonal coverages include:

• Validation - check that a set of discrete polygons forms a valid coverage
• Gap Detection - check if a polygonal coverage contains narrow gaps (using a given distance tolerance)
• Cleaning - fix errors such as gaps, overlaps and slivers in a polygonal dataset to ensure that it forms a clean, valid coverage
• Simplification - simplify (generalize) polygon boundary linework, ensuring coverage topology is preserved
• Precision Reduction - reduce precision of polygon coordinates, ensuring coverage topology is preserved
• Union - merge all or portions of the coverage polygons into a single polygon (or multipolygon, if the input contains disjoint regions)
• Overlay - compute the intersection of two coverages, producing a coverage of resultant polygons 

Implementing polygonal coverage operations is a current focus for development in the JTS Topology Suite.  Since most operations require a valid coverage as input, the first goal is to provide Coverage Validation.  Cleaning and Simplification are priority targets as well.  Coverage Union is already available, as is Overlay (in a slightly sub-optimal way).  In addition,  a Topology data structure will be provided to support the edge-node representation.  (Yes, the Topology Suite will provide topology at last!).  Stay tuned for further blog posts as functionality is rolled out.

As usual, the coverage algorithms developed in JTS will be ported to GEOS, and will thus be available to downstream projects like PostGIS.

JTS 1.19 Released

JTS 1.19 has just been released!  There is a great deal of new, improved and fixed functionality in this release - see the GitHub release page or the Version History for full details.

This blog has several posts describing new functionality in JTS 1.19:

New Functionality

• Concave Hull of Polygons
• Algorithm for Concave Hull of Polygons
• Outer and Inner Concave Polygon Hulls
• Using Outer Hulls for Smoothing Vectorized Polygons
• Concave Hulls
• Polygon Triangulation
• Cubic Bezier Curves
• Offset Curves

Improvements

• KD-tree query performance improvement with randomized insertion

Many of these improvements have been ported to GEOS, and will appear in the soon-to-appear version 3.11.  In turn this has provided the basis for new and enhanced functions in the next PostGIS release, and will likely be available in other platforms via the many GEOS bindings and applications.

Algorithm for Concave Hull of Polygons

The previous post introduced the new ConcaveHullOfPolygons class in the JTS Topology Suite.  This allows computing a concave hull which is constrained by a set of polygonal geometries.  This supports use cases including:

• generalization of groups of polygon
• joining polygons
• filling gaps between polygons

A concave hull of complex polygons

The algorithm developed for ConcaveHullOfPolygons is a novel one (as far as I know).  It uses several features recently developed for JTS, including a neat trick for constrained triangulation.  This post describes the algorithm in detail.

The construction of a concave hull for a set of polygons uses the same approach as the existing JTS ConcaveHull implementation.  The space to be filled by a concave hull is triangulated with a Delaunay triangulation.  Triangles are then "eroded" from the outside of the triangulation, until a criteria for termination is achieved.  A useful termination criteria is that of maximum outside edge length, specified as either an absolute length or a fraction of the range of edge lengths.

For a concave hull of points, the underlying triangulation is easily obtained via the Delaunay Triangulation of the point set.  However, for a concave hull of polygons the triangulation required is for the space between the constraint polygons.  A simple Delaunay triangulation of the polygon vertices will not suffice, because the triangulation may not respect the edges of the polygons.  

Delaunay Triangulation of polygon vertices crosses polygon edges

What is needed is a Constrained Delaunay Triangulation, with the edge segments of the polygons as constraints (i.e. the polygon edge segments are present as triangle edges, which ensures that other edges in the triangulation do not cross them).  There are several algorithms for Constrained Delaunay Triangulations - but a simpler alternative presented itself.  JTS recently added an algorithm for computing Delaunay Triangulations for polygons.  This algorithm supports triangulating polygons with holes (via hole joining).  So to generate a triangulation of the space between the input polygons, they can be inserted as holes in a larger "frame" polygon.  This can be triangulated, and then the frame triangles removed. Given a sufficiently large frame, this leaves the triangulation of the "fill" space between the polygons, out to their convex hull. 

Triangulation of frame with polygons as holes

The triangulation can then be eroded using similar logic to the non-constrained Concave Hull algorithm.  The implementations all use the JTS Tri data structure, so it is easy and efficient to share the triangulation model between them. 

Triangulation after removing frame and eroding triangles

The triangles that remain after erosion can be combined with the input polygons to provide the result concave hull.  The triangulation and the input polygons form a polygonal coverage, so the union can be computed very efficiently using the JTS CoverageUnion class.  If required, the fill area alone can be returned as a result, simply by omitting the input polygons from the union.

Concave Hull and Concave Fill

A useful option is to compute a "tight" concave hull to the outer boundary of the input polygons.  This is easily accomplished by removing triangles which touch only a single polygon.  

Concave Hull tight to outer edges

Concave Hull of complex polygons, tight to outer edges.

Like the Concave Hull of Points algorithm, holes are easily supported by allowing erosion of interior triangles.

Concave Hull of Polygons, allowing holes

The algorithm performance is determined by the cost of the initial polygon triangulation.  This is quite efficient, so the overall performance is very good.

As mentioned, this seems to be a new approach to this geometric problem.  The only comparable implementation I have found is the ArcGIS tool called Aggregate Polygons, which appears to provide similar functionality (including producing a tight outer boundary).  But of course algorithm details are not published and the code is not available.  It's much better to have an open source implementation, so it can be used in spatial tools like PostGIS, Shapely and QGIS (based on the port to GEOS).  Also, this provides the ability to add options and enhanced functionality for use cases which may emerge once this gets some real-world use.