A common spatial need is to compute a polygon which contains another set of polygons. There are numerous use cases for this; for example:
- Generalizing groups of building outlines (questions: 1, 2)
- Creating "district" polygons around block polygons (questions: 1)
- Removing gaps between sets of polygons (questions: 1, 2, 3, 4)
- Joining two polygons by filling the space between them (questions: 1, 2)
Approach: Convex Hull
The simplest way to compute an area enclosing a set of geometries is to compute their convex hull. But the convex hull is a fairly coarse approximation of the area occupied by the polygons, and in most cases a better representation is required.
Here's an example of gap removal between two polygons. Obviously, the convex hull does not provide anything close to the desired result:
Approach: Buffer and Unbuffer
A popular suggestion is to buffer the polygon set by a distance sufficient to "bridge the gaps", and then "un-buffer" the result inwards by the same (negative) distance. But the buffer computation can "round off" corners, which usually produces a poor match to the input polygons. It also fills in the outer boundary of the original polygons.
Approach: Concave Hull of Points
A more sophisticated approach is to use a concave hull algorithm. But most (or all?) available concave hull algorithms use points as the input constraints. The vertices of the polygons could be used as the constraint points, but since the polygon boundaries are not respected, the computed hull may cross the polygon edges and hence not cover the polygons.
Densifying the polygon boundaries helps, but introduces another problem - the computed hull can extend beyond the outer boundaries of individual polygons. And it introduces new vertices not present in the original data.
Solution: Concave Hull of Polygons
What is needed is a concave hull algorithm that accepts polygons as constraints, and thus respects their boundaries. The JTS Topology Suite now provides this capability in a class called ConcaveHullOfPolygons (not a cute name, but descriptive). It provides exactly the solution desired for the gap removal example:
The Concave Hull of Polygons API
Like concave hulls of point sets, concave hulls of polygons form a sequence of hulls, with the amount of concaveness determined by a numeric parameter. ConcaveHullOfPolygons uses the same parameters as the JTS ConcaveHull algorithm. The control parameter determines the maximum line length in the triangulation underlying the hull. This can be specified as an absolute length, or as a ratio between the longest and shortest lines.
Further options are:
- The computed hull can be kept "tight" to the outer boundaries of the individual polygons. This allows filling gaps between polygons without distorting their original outer boundaries. Otherwise, the concaveness of the outer boundary will be decreased to match the distance parameter specified (which may be desirable in some situations).
- Holes can be allowed to be present in the computed hull
- Instead of the hull, the fill area between the input polygons can be computed.
Examples of Concave Hulls of Polygons
Here are examples of using ConcaveHullOfPolygons for the use cases above:
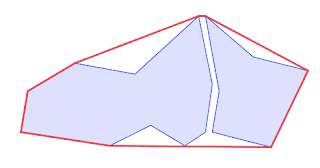
Example: Generalizing Building Groups
Using the "tight" option allows following the outer building outlines.















No comments:
Post a Comment