- efficiently enumerating all vertices in the QuadEdge data structure which provides the basis for Delaunay computation
- computing the circumcentre of all Delaunay triangles in a consistent way
- clipping the generated Voronoi cell polygons to a reasonable bounding area)
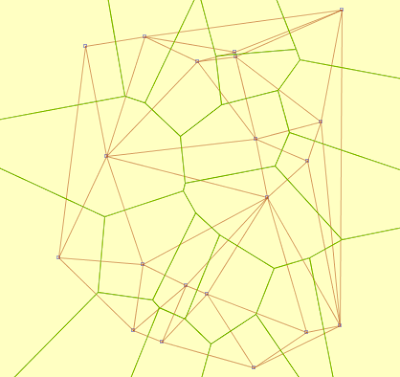
Delaunay and Voronoi diagrams of 20 points (15 ms)

Voronoi diagram of 100 points (63 ms)

Voronoi diagram of 100,000 points (7.3 sec)
The JTS implementation scales very well - a Delaunay/Voronoi diagram of 1 million points computes in under 5 minutes. The one downside is memory usage. As usual, Java is quite memory-hungry - a 1 M point Delaunay takes around 700 MB. This seems excessive, even for Java. Hopefully some memory profiling may reveal that this can be reduced by some tuning of the class structures involved.
Even better, the Delaunay/Voronoi algorithm seems to be quite robust, even though no special attempt has been made to provide high-precision or otherwise robust implementations of some of the key predicates (inCircle and orientation). This may yet prove to be an issue for some inputs, but at this point it seems possible to claim that for non-pathological inputs the algorithms execute correctly.







8 comments:
Martin,
This sounds great. Would be nice to see this make it into GEOS and PostGIS. Wonder how far down the line that would be.
Good question, Regina. Probably depends on whether and when funding appears...
But perhaps now you are a highly paid author you will be interested in chipping in - especially if it means more content for your next edition? 8^)
Highly paid :) Well depends what your idea is of highly paid. But we'll see if there is enough demand for the book, we will cheap in some of our royalty.
Hmm I mean chip in.
have you seen this demo ?
http://www.emgu.com/forum/viewtopic.php?f=2&t=245
I was using sharpmap and NTS but This is unfortunately dependant on the algorithm of EmguCV.
Agelos,
No, I haven't seen the demo. Do you have any screenshots from it?
Perhaps the JTS Voronoi code will get ported to NTS someday...
Martin, great work. Would it be possible to provide a link to the code that actually computes the voronoi polygons? Here or maybe on the jts mailing list. Thanks heaps, Martin T.
Martin,
The Voronoi code will be released in JTS 1.11. I'm hoping to get this out soon, but in the meantime you can access the code from the JTS CVS repository. Check this page for details:
http://tsusiatsoftware.net/jts/main.html
Post a Comment