Improvements to robustness in JTS Delaunay Triangulation

JTS 1.11 added the capability to compute Delaunay Triangulations of point sets. Although the triangulation code was extensively tested and used prior to release, it unfortunately didn't take long before someone uncovered a robustness issue. The problem occurred in a large dataset of over 288,000 points. When the JTS 1.11 Delaunay algorithm was run against this data, a TopologyException was thrown, preventing the computation from completing.

Here's a portion of the dataset which produced the problem:



Digging into the code , it turned out (not unexpectedly) to be caused by a robustness failure in the inCircle predicate. InCircle is a key test used in Delaunay triangulation. The standard algorithm for computing it involves determining the sign of the determinant of a 4x4 matrix.


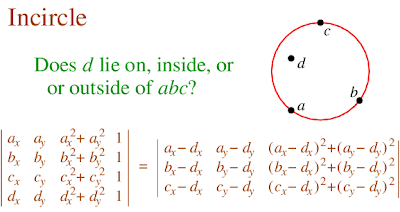
This computation is notoriously prone to robustness failure when evaluated using double-precision arithmetic. The rounding errors inherent in using double-precision can cause the sign of the determinant to be computed incorrectly. (For an good explanation of the issue see this page by Jonathan Shewchuk.)

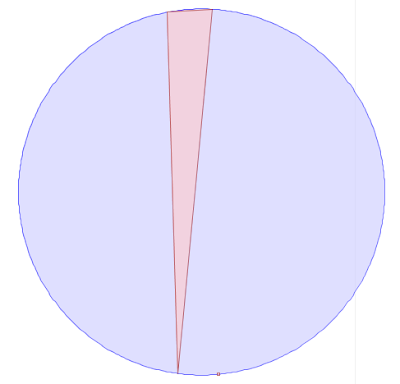
As a concrete example, consider testing whether the point

POINT (687958.13 7460720.99)

lies in the circumcircle of the triangle

POLYGON ((687958.05 7460725.97, 687957.43 7460725.93, 687957.58 7460721, 687958.05 7460725.97)

Visually this looks like:

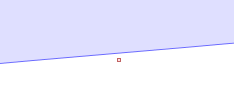
Zooming in, you can see that the query point is NOT in the circumcircle, so that InCircle()=FALSE.

However, evaluating the inCircle predicate determinant using double-precision computes InCircle()=TRUE. This is because the large magnitude of the ordinate values relative to the size of the triangle causes the significant information to be lost in the roundoff error. The effect of this error propagates through the Delaunay algorithm. Ultimately this results in a convergence failure which is detected and reported.

Luckily, a solution was immediately to hand, in the form of the DoubleDouble extended-precision library I ported to Java a while ago. Re-implementing the predicate evaluation using DoubleDouble computed the correct results for inCircle in all cases. This eliminated the robustness failure, and allowed the Delaunay Triangulation of the entire 288K point dataset to be computed without errors (for the record, this took 5 min 20 s).


The DoubleDouble code had been a solution in search of a problem for quite a while, so I was happy to get to prove its usefulness in a real-world situation.

And the story doesn't end there - it gets even better...