New Buffer Styles in JTS 1.9

JTS allows specifying styling parameters to control the appearance of generated buffer polygons.

End Cap styles have been available for a while. End caps can be Round (the default), Flat, or Square. For Round caps, the Quadrant Segments parameter controls the degree of approximation to a true circular arc.

End Cap Styles: Round, Flat, Square

JTS 1.9 adds the ability to specify the Join Style. The Join style controls how the offset curves for consecutive line segments are joined together. The Join type can be Round (the default), Mitre, or Bevel. If Mitre is specified, a further Mitre Limit parameter is provided to control how long mitred joins can be before they are beveled off. The maximum length of a mitred corner is equal to the Mitre Limit multiplied by the buffer distance.

Join Styles: Mitre (limit = 10), Mitre (limit = 1), Bevel

The JTS TestBuilder has been enhanced to allow specifying all of these parameters, so it can be used to experiment with the visual effects of the various styles.

Hey What's That - Terrain Panoramas Mashup

Here's a nifty mashup using Google Maps. It computes a skyline terrain panorama from a given location.



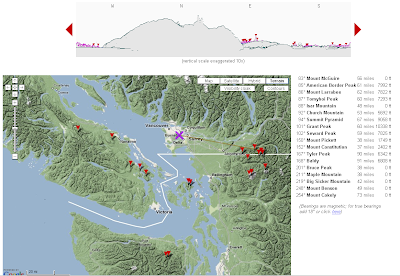
The computed skyline isn't bad, although a bit optimistic (I'm pretty sure you can't see the Olympics from downtown Vancouver!). I think this particular query is ignoring earth curvature (although apparently you can choose to take it into account.)

The site uses it's own SRTM dataset. The gazetteer is impressive - not sure how they get that information.

Cross-Border issues with Google Maps terrain

So GM now has terrain - yay! But they seem to have short-changed half the continent. Check this screenshot from the border just south of Chilliwack. Notice the American Border Peak - but where's the Canadian one? And what's with that crazy-looking border swathe?


I assure US viewers that Canada isn't normally this blurry. And no, it isn't proof that we really do have a year-round 4 ft snowpack!

Ok, I know - never satisfied. Really, this is a very nice feature. I just hope Google gets their north-of-the-border vision lasered real soon...

Enumerating permutations using inversion vectors and factoradic numbering

Permutations are a fundamental concept in discrete mathematics, and crop up in numerous places in computer science. The set of all possible permutations of n items is usually denoted S_n (since the set forms a group which is isomorphic to the Symmetric group of order n). The number of permutations in this set is n!.

This apparently simple concept poses some unexpected challenges. For instance, the following useful operations are messy to compute via the brute-force way of enumerating successive permutations:

• List all the permutations in S_n (in lexicographic order)
• Find the i'th permutation in S_n

This would be straightforward if there was a way of effectively enumerating all permutations; i.e. a mapping between S_n and the integers {1, 2, ..., n!}.

It turns out that this can be done using a pair of ingenious concepts known as the inversion vector and factoradic numbering. These can be used to provide an enumeration of S_n, conveniently in lexicographic order. (Inversion vectors are also known as inversion tables and Lehmer codes - the term vector seems to me to be most appropriate for the nature of the structure.)

A permutation can be written as a sequence of numbers

P = (p₁ p₂ ... p_n) where p_i is in {1, 2, ..., n}

An inversion is a pair (p_i, p_j) where i < j but p_i > p_j. We define d_i to be the number of inversions in the sequence where the first element is p_i:

d_i = | { p_j : i < j , p_i > p_j } |

Then the inversion vector for the permutation is the sequence

D = (d₁, d₂, ..., d_n) (d_i is in the range {0, 1, ..., n-i})

It is fairly straightforward to recover the original permutation from the inversion vector. This paper gives a definition of the forward and reverse mapping algorithms.

There are n! possible sequences D. They are in one-to-one relationship with the set of permutations S_n, and their natural order gives a lexicographic ordering of S_n. So we're halfway to the enumeration that we are looking for.

Inversion vectors can in turn be mapped to the integers in {1, ..., n!} by using the concept of factoradic numbering. A factoradic number is a number made up of a sequence of digits where the radix for digit d_i is (n-i)!. This Wikipedia article explains the concept in detail.

Here's an example:

P = (4 6 2 5 3 1 8 7) is a permutation in S₈.

Its inversion vector is L(P) = [3,4,1,2,1,0,1,0].

The factoradic representation of this is

3×7! + 4×6! + 1×5! + 2×4! + 1×3! + 0×2! + 1×1! + 0×0! = 18175

So inversion vectors and factoradic numbering provide an elegant way of enumerating permutations. But what does this have to do with geospatial processing? That will be a subject for another post...

If programming languages attended computer conferences

If you're a language geek, this post by David Rupp is hilarious!

Fast polygon merging in JTS using Cascaded Union

A common requirement in spatial processing is to union a set of polygons together. Depending on the use case, the polygons may either be a coverage or be overlapping. Up until recently, there were two techniques for accomplishing this in JTS:

• Iterated Union: Iterate over the polygons and union them one-by-one into a result polygon
• Buffer Union: Collect the polygons into a GeometryCollection and run buffer(0) on the collection

The first one is straightforward, but quite inefficient for large input sets. The second technique is more efficient in many cases, but still tends to fail for large or complex data.

Since this is such a common operation, I've been keen to find a faster and more robust approach. An alternative strategy is to use a concept I call Cascaded Union. The idea is to union small subsets of the input together, then union groups of the resulting polygons, and so on recursively until the final union of all areas is computed. This can be thought of as a post-order traversal of a tree, where the union is performed at each interior node. If the tree structure is determined by the spatial proximity of the input polygons, and there is overlap or adjacency in the input dataset, this algorithm can be quite efficient. This is because union operations higher in the tree are faster, since linework is "merged away" from the lower levels.

This picture shows the algorithm in action:


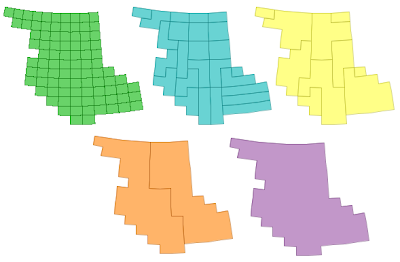
Handily, the spatial indexes already in JTS can be used to determine an appropriate tree structure. Currently the Sort-Tile-Recursive packed R-Tree index is used - this seems to produce an effective tree (although I suspect that the algorithm is not very senstive to the precise spatial tree used)

It turns out that Cascaded Union can be much more efficient than Iterated Union. On a test dataset with 30,000 small polygons with a high degree of overlap, the performance results were:

Cascaded Union: 20 sec
Iterated Union: 3 hours 40 min !

Not bad - well worth the effort of coding... Also, it's more robust than Buffer Union, and often much faster as well.

This will be provided via the Geometry.union() (Unary union) method in JTS 1.9.

Implementations of Polygon Overlay algorithms

Occasionally people ask about the algorithms used in JTS's overlay operations. I don't have a good answer for this, since I basically made it up (in an informed kind of way), and haven't had time to document it to the level I'd like (thank goodness for self-documenting code... 8^)

I recently came across this web site from back in 1998, which is happily still around. It has a good list of implementations of what it calls Polygon Boolean operations. (This is the same thing as the JTS overlay operations - I chose to use a different term to avoid confusion with the spatial predicates). Perhaps some of these sites have done a better job of documentation! There's also some useful references to academic papers covering aspects of the issue.

The bible of Spatial Indexing

The Bhagavad Gita of Multidimensional Access Methods...
The Koran of Quadtrees...

One of the people I met at ACM GIS 2007 was the conference chair, Hanan Samet. He's published a series of highly useful books on spatial indexing methods, which are certainly the most comprehensive and detailed in this field. His latest work is Foundations of Multidimensional and Metric Data Structures and is surely his magnum opus. It could also be called Everything you wanted to know about Spatial Indexes (but were afraid to code). Recommended reading for spatial geeks, especially if you're looking for some reading to tide you over during your next year off.

His first book on the subject, The Design and Analysis of Spatial Data Structures, is also worth looking at, especially since it's a bit more bite-sized. However, it's out-of-print, and expensive when you do find a copy (local plug: I found mine through ABE) If you really can't find a copy you might try contacting Hanan directly.

Hanan has a clear preference for quadtree structures over R-trees, but both approaches are covered well (including pseudo-code - yay!)

Conference Review: ACM GIS 2007

I just got back from ACM GIS 2007, over in Seattle. This is the first time I've attended this conference - or even known about it! It was a good year to go, since there was a lot of energy in the air due to this being the first year that the conference has been held as an independent event in its own right (which may be one reason I haven't heard of it before). One reason for doing this is to catch the building geospatial wave - more on this below.

The conference was very well attended (about 200 people). The bulk of attendees seemed to be from US universities - but hailed from all over the globe. Microsoft was there in force, as you might expect, and Google was very prominent too (a running joke at the conference was that every talk was connected to or given by someone tied to MS or Google). The omnipresent Michael Jones gave a good motivational talk about some of the technologies which are challenges for Google and would be fruitful research areas. Clearly the big guns of the GeoWeb are investing heavily in geospatial research, and this in turn is injecting a lot of cash and relevancy into this field.

Some of the presentations which stood out for me were:

• Using Constraint Programming to conflate address data to urban imagery. Constraint programming is a well established "AI" technique with a lot of mature effective algorithms, and it seems like a promising approach for other kinds of conflation problems as well (such as road network conflation)
• A guy from Google talked about conflating vector road networks to ortho imagery (surprise, surprise - this is a big use case for them). His approach seem to take place mostly in the raster domain (using edge detection and signal isolation), which I found interesting
• A talk by Andrew Danner about building massive TINs and extracting drainage patterns from them. Having just tackled a very similar problem (in both domain and data size) I was interested to see his approach - which was a fair bit more clever. His group has a novel external memory algorithm for building TINs on huge datasets. This seems like an important focus for research, since data gathering bandwidth is outpacing RAM growth.
  
• A couple of talks on approaches for compressing surface models and extracting varying levels of detail. Nice because they used some elegant mathematical concepts such as Morse-Smale codes.

There were lots of other talks - and a HUGE bonus was that the conference proceedings were provided to you at registration time (not 2 months later). So you could read ahead to get a good idea of what was coming up - or use downtime to get a more in-depth understanding of a previous talk.

Speaking of which, this is the first conference I've been to which had a single track of presentations. This made for pretty full days, and was probably only barely possible due to the size of this conference, but it certainly made for a more satisfying, less stressful, and more inclusive experience. No need to agonize on which one of 5 presentations might be the most interesting and then rush madly around repositioning during the 5-min break between talks. And it gave you time to catch up on your reading if the subject wasn't of total interest.

Next year the conference is in Irvine, CA. The organizers are keen to get more industry participation, so don't be shy - check it out.

Workaround to Google 4 Black Screen Of Death problem

Ever since I upgraded to Google Earth 4, I've had the extremely annoying problem that tilting to an oblique view produced a completely black screen. The only way to get the screen view back was to restart GE. Time to dust off that ol' BSOD acronym...

I just found a thread which provides a clue to why the problem occurs, and gives a workaround (which doesn't 100% remove the annoyance, since it only works for that one session).

Apparently the problem is caused by the use of a dual core AMD Athlon processor. The solution is to set the processor affinity to use only a single core for the GE process. (TaskManager, Processes Tab, rightclick process 'googleearth.exe', 'Set Affinity', select 1 processor only). I haven't yet found a way to persist this setting - anyone have any ideas?


Update: After a few milliseconds more browsing, I found that you can use the imagecfg.exe utility to permanently set the processor affinity for a load image. Running the following command in the Google Earth directory does the trick:

imagecfg -a 0x1 googleearth.exe

Virtual nautical sightseeing around Victoria

The great thing about living on an island in the Pacific Ocean is that you're surrounded by... well, ocean. And the great thing about oceans is that there's always something going on. So much goes on, in fact, that Google manages to capture some of it on their infrequent satellite flyovers. Here's a couple of interesting events:

• A nuclear submarine on its way home to Bangor. I'm happy to see that it's clearly making pretty good time, so if one of those warheads did happen to tip over it might be far enough away that we'd only hear the bang and get a bit of a suntan. And according to Google's yellow line it's keeping to its side of the street, which is a good thing too - a head on collision with a container ship would probably substantially lower the property values in my neighbourhood.
• An apparently sinking ferry. No surprises really, we've had a bit of that going around recently. Hopefully everyone made it off this one, so as not to spoil B.C. Ferries' almost perfect record for the last two years. Never mind, we'll get the Germans to build us another one.

You have to really like this neogeography stuff, it's such a time-saver - I no longer have to walk two blocks to watch for nuclear submarines. And maybe take the ferry less often too, which is also good for the health!

Geometry Safari - Squircles, Supercircles, and Superellipses

Everyone knows that the equation of a circle is the beautifully simple:

x² + y² = C

An obvious generalization of this is to allow higher values for the exponent:

|x|ⁿ + |y|ⁿ = C : n >= 2

This produces a family of nicely rounded closed curves which are asymptotic to squares. For n = 4 the curve looks like this:

x⁴ + y⁴ = C

It turns out this geometric shape has been given a cute name: squircles (Who said geometry has to be dull?) The entire family is known as supercircles. And of course, there is a analogous generalization for ellipses known as superellipses. (I don't think there's a "sqellipse", however - and maybe that's just as well).

This page allows you to generate supercircles for different values of n. (Incidentally it uses Walter Zorn's very slick jsGraphics library for generating pixel & vector graphics on web pages).

Useful? Sort of - Wikipedia has a few examples, mostly in the decorative arts. And I'm betting that a concept this elegant is bound to turn up in lots more places. So maybe I should add this to JTS, just to - ahem - get ahead of the curve.

En l'an 2000

The Bibliotheque Nationale de France has an online exhibition of a vision of the world in the year 2000 - published in the year 1910. It's interesting to see what the artist got right, and what he got wrong. Air-Sea Rescue - but also radium fireplaces. He correctly predicted that electric power would replace human labour - but he didn't foresee that the biggest impact would be from automating thought rather than muscle.

He also didn't see that the fashions of 1910 would not be a la mode in 2000. But it's an appealing vision... I'm still hoping for my personal monoplane to get me to work.

Bursa-Wolf transformations explained

.. courtesy of Adrian Custer on the OpenJUMP mailing list:

> > just one question .. what is this bursa wolf parameter option?

> My impression is that this is scary math I never quite understood.




Well, Bursa was a 9 year old bicyclist from the Alps and...no, no, no, i
lie. Actually it's not particularly scary math and quite easy to
understand. All you really need to remember is that no one has ever been
to the center of the earth.



So everyone started surveying (mostly so the repressive central
governments could exploit taxes from people and have lots of jolly wars
where people could slog through the mud and kill each other so they'd be
blood and suffering for all). Each group started from some random place
on the surface of the earth. Right away, it becomes obvious to everyone
that euclidean rules don't work so well. Some didn't care so much since
taxes are basically arbitrary anyway and getting serious about it means
you'd have to walk through fields and woods and get lots of mud on your
shoes. Others kept at it and resorted to spherical geometry. Once you
start doing that precisely and at continental scales you realize that
doesn't really work either so you decide to try the next hardest thing,
an ellipsoid of rotation. Now how do you know which one to choose? Well
you pick one that minimizes your squared errors. All good and nice but
(1) you are surveying the ground which is anything but an ellipsoid
since it has all those ditches you keep falling into and that keep
getting your clothes covered in mud and (2) you are not perfect
especially with all that mud on your paper. So you have a bunch of
errors. Well everyone that does this comes up with lots of different
ellipsoids that work really nice for their data and everyone is sure
they clearly have found the 'one true ellipsoid' and they decide to use
that for all their work. Then everyone guesses where they actually are
on each of their particular ellipsoids which involves lots of going
outside at night and looking up from the mud at the stars. But then it's
not like the edges of each survey was nice and level on these ellipsoids
either --- think of the eastern USA. You can start nice and clean and
warm and dry at an inn in Boston on the edge of the sea drinking clam
chowder and having a good time but a few months later it will be bitter,
bitter cold in that tiny town of Denver because you are somewhere like a
mile high up in the air and you're wet and covered in mud from slogging
through the plains in a snowstorm. So you've got a pretty good idea that
your data is on a major slant but, well, you'll do your best to make up
for it but it really doesn't help the effort any, especially what with
all that mud that's still itching in your hair. So your errors may be a
wee bit big but hey it's all right: it's good enough to wage lots of
good wars with lots of mud and blood and to keep collecting lots of
taxes so no one cares too much.



Fast forward to more recent times where some people want to talk to lots
of different governments and work with lots of different data. They take
everyone's guess and try to line them up. Well it turns out, when you
try to line everything up, that the center points of all the different
ellipses aren't really the same points and even the orientation of the
three axes are all a bit off because of how everyone guessed where their
were on their ellipsoids. So now, to go from one data set to another so
they line up "the best," you need estimates of how much to rotate each
of the axes and how to shift the center point around; all this beyond
even the obvious stuff of changing between the different definition of
all those "one true" ellipsoids.



When you do this mathematically, you need a bunch of parameters: these
now have the names of the wolf and the bursa. Generally, you can only
come up with good parameters if you have lots of data to compare and
some good software to do the comparing. That's what the EPSG did for
everyone. The guys in the pickup trucks that went out looking for oil
kept falling into ditches along the way and getting mud on their faces
but when they got back to the office they had a good sense of what lined
up with what and could say: "yep, that hill there is the same as this
squiggle here and there's this big ditch right here that cost us our
third flat tire and..." So they collected as much data as they could and
compared it and came up with a database of parameters by which you go
from one data set to another. So that's it. That's why we use their
data; we don't have to fall in any ditches and can avoid getting mud on
our clothes. They give us their parameters and we can mostly line up
data from one survey against data from another. But you do need some
good parameters because the earlier folk had a harder time of the mud
and the data they created don't just line up the way we would like them
to.



Actually doing the math is a bit harder but the concept is pretty
straight forward: geographic data all ultimately gets tied into points
on the earth surface and that requires estimating where the points
really are and how they line up on the estimated ellipsoid being used.
That in turn means none of ellipsoids quite line up and we need
parameters to move between them.



--adrian

Office 2.0

Office 2.0 is an index of Web-hosted applications. The entire list is pretty overwhelming, but more immediately interesting is the list of Web apps that the site's creator uses as his "everyday applications"

Maybe there's something to this Web thing after all...

Late notice: Waterfall 2006 conference on Project Management

Here's an important conference which unfortunately I missed last year. But no matter - the content is timeless, so no doubt it will be held over and over again with exactly the same presentations.

Quote of the day - C. A. R. Hoare

There are two ways of constructing a software design: One way is to make it so simple that there are obviously no deficiencies, and the other way is to make it so complicated that there are no obvious deficiencies. The first method is far more difficult.

- C. A. R. Hoare

Geodetic data in PostGIS - Spherical indexing schemes

Here at Refractions we're starting to think about how we can provide better support in PostGIS for geodetic data. Geodetic data is data which is defined in a true spherical coordinate system (in particular, of course, the surface of the Earth).

Currently PostGIS provides some geodetic-aware functions (such as distance between two geodetic points). But it's current spatial data model is fundamentally planar, so there are definite limitations to modelling geodetic data (e.g. such as the notorious "line crossing the Date Line" problem). As PostGIS gets used for larger datasets and more ambitious projects, the utility of having a full-function geodetic data model is becoming increasingly obvious.

Handling geodetic data in a correct and efficient way presents quite a few challenges. A major one is: how can geodetic geometry be spatially indexed? Conventional spatial indexes (such as 2D R-trees) all rely on geometry being embedded in a planar space. They don't handle data which can "wrap around", as can occur in a spherical space.

There have been various clever proposals for spherical indexing strategies. Some prominent ones are listed below:

• Hierarchical Triangular Mesh - this is essentially a "quad-tree for the sphere". It has a lot of appeal for use with point data, since it provides a hierarchical key which can be indexed using a conventional B-tree index. (It was co-developed by the late, great Jim Gray in order to index astronomical data). The mathematics to determine the index key for a non-point object would seem to be somewhat complicated. It also seems like HTM would suffer from the usual disadvantage of quadtrees of not being very self-tuning. Another disadvantage from the PostGIS point of view is that this would likely be a brand new index type (i.e. lots of difficult code to write)

• Hipparchus Voronoi-based index. This index can be thought of as a fixed-grid index using a custom Voronoi cell coverage for the globe. IBM's DB/2 Geodetic extension uses this scheme. I must say that this concept, while ingenious, seems a bit baroque to me. This index has the usual disadvantage of fixed-grid indexes of not handling widely-varying data sizes well. And it also requires extremely complex cell coverage structures, which have to be selected specifically for the expected data composition. DB/2 supplies 13 different ones based on various data densities (G7 industrial output, anyone?). I'm not sure what you are supposed to do if your data has some other density distribution - it doesn't seem very feasible to make your own Voronoi grid. And what if you don't know your data distribution, or it changes over time?
  

• 3D Bounding Box - this is the approach used by the pgSphere project. It's pretty straightforward. The key concept is to embed the sphere in 3-space, so that it is possible to compute 3D bounding boxes for geometries on the embedded sphere. The bounding boxes can then be indexed using a 3D R-tree (exactly analogous to a 2D R-tree spatial index). The GIST index supplied with PostgreSQL can be customized to provide the required 3D R-tree. One possible issue is that apparently R-trees become "less effective" in higher-dimensional spaces. It remains to be seen whether this is truly a serious problem.
  

Out of these options, it seems like the 3D Bounding Box approach is the most straightforward scheme. There's some challenges in developing the mathematics required (at least, for a planar/linear guy like me), but I'm hopeful that we can deal with these issues and arrive at a efficient, maintainable solution.

If REST and WS-* are at war, which one are they fighting?

Ted Nedward has another great post providing lessons about technical, political and historical issues all at the same time.

Let's just hope it isn't the Hundred Years War instead...

Grokking hierarchical queries in Oracle

Oracle provides a very powerful SQL extension to evaluate hierarchical queries (transitive closures) on tables. This recently saved my bacon in a system which processed a table modelling a tree containing several hundred thousand rows. The alternative would have been to do some very ugly and inefficient iterative querying.

There's a few tutorials about Oracle hierarchical queries on the Web, but I didn't find any of them gave me a good mental model of how these queries are evaluated. In particular, they didn't really help me in figuring out how to traverse a tree structure either upwards or downwards. So here's my attempt at explaining some patterns for using hierarchical queries. (This isn't a complete tutorial - for that check the Oracle 10g documentation)

For modelling tree-structured data, the usual pattern is to have a table with id and parent_id columns. In a hierarchical query you may wish to traverse the tree either upwards (towards the root(s)) or downwards (towards the leaves). But what query syntax should be used to produce the desire direction?

The general syntax for CONNECT BY is:

CONNECT BY [PRIOR] col1 = [PRIOR] col2

A further constraint is that the PRIOR keyword can appear once only, but it can appear on either side of the equality condition. Since the equality condition is symmetric, there are really only two possibilities:

1. CONNECT BY PRIOR parent_id = id (which is equivalent to CONNECT BY id = PRIOR parent_id)
2. CONNECT BY PRIOR id = parent_id (which is equivalent to CONNECT BY parent_id = PRIOR id)

Oracle evaluates the hierarchical query in the following way:

1. The result rowset is initialized with the rows determined by the START WITH clause
2. All rows for which the CONNECT_BY condition is true are added to the result rowset. The PRIOR keyword determines which one of the condition expressions is evaluated in the context of the result rowset rows.
3. Step 2 is repeated until no further rows match.

Formally, this procedure computes the transitive closure of the relation defined by the initial START WITH set and the CONNECT BY condition.

Given this evaluation rule, we obtain the following rule-of-thumb for writing a query to traverse in a desired direction:

• To traverse upwards, use form #1
• To traverse downwards, use form #2

There's several other useful parameters for defining hierarchical queries in Oracle, such as NOCYCLE, LEVEL, CONNECT_BY_ROOT, CONNECT_BY_ISLEAF, etc. It's well worth studying how to use these to improve query power and performance.

Natural Docs for code documentation generation

Natural Docs looks like a nice generator for code documentation. It's multi-language, with a more natural commenting style than Javadoc. It seems to be in fairly steady development, and has a slick homepage.

A quick browse of Wikepedia reveals a zillion documentation generators. This isn't really a surprise - once again the OSS ecosystem thoroughly fills a technological niche! Robodoc and Doxygen are other leading players. Wikipedia is (rightly) very neutral in its comparison. I'd be interested to learn if there is a reason to prefer one more than the others (say, from the point of view of wanting to support a new language).

The need for complex types in XML schema languages

Sean left a comment referring to a post by James Clark on TEDI, a new kind of schema language for XML. It's a very interesting post. I like how it elevates the issue to one of defining a common data meta-model, with mappings to the plethora of formats which are all basically trying to do the same thing (XML, JSON, YAML, etc).

However, I think I noticed something missing in the TEDI concept. This is the ability to define complex types which are composed of combinations of basic data structures. XML Schema of course does have this feature, and it's responsible for a significant part of the perceived complexity. But a schema language which lacks this ability is limited in its expressiveness. A sterling example is GML Geometry. Geometric types are complex enough that they have to be defined in terms of simpler XML data structures. One of the goals of GML is to provide a meta-schema which defines the concept and structure of expressing geometric datatypes in XML. To accomplish this, the concept of a Geometry datatype needs to be expressible at the schema level.

Of course, for any given application domain you can dodge this issue by simply relying on convention. A datatype with more than trivial semantics is going to have a custom implementation in any given system, so a custom mapping from XML will be needed in any case. But that's not really the point - surely at this stage of computer science we can do better than arbitrary convention?

I haven't yet seen an explanation of whether RELAX-NG provides this level of expressiveness. I don't see it in JSON or YAML. But it seems like this capability is essential for any schema language which is going to take us beyond simply collections of a small set of datatypes.

RELAX NG good, XML Schema bad?

Here's a nice post on why RELAX NG is better than XML Schema. Since data modelling and language expressiveness are a major interest, I'm finding it fascinating to watch the evolutionary battles in the world of "meta-XML".

One key point made is that RNG is much easier to grasp than XML Schema. Witness this short tutorial which tells you most of what you need to know.

Something I haven't fully understood yet is why RNG fans consider PSVI to be a bad idea. As far as I see, any tool which is a general purpose parser for typed XML is going to have to define a metamodel describing the allowable range of documents. Doesn't it make sense to have a standard model for this?

Another thing I don't see is whether and how RNG supports the constrained extensibility of schemas (i.e. subclassing). This is responsible for a fair bit of the complexity in XML Schema, but is essential in some uses (such as GML, which is really a schema framework for defining other concrete schemas).

Probably the most appealing aspect of RNG is its compact syntax. It's much more readable than XML. (XML is a terrible syntax for expressing a hierarchical language!). Of course, this means the end of the "one parser to scan them all" dream - but perhaps that's a good thing. Come back, YACC, we really didn't mean it and we still love you!

This post gives a rebuttal to the RNG-over-XSD argument. He seems to think that RNG lacks subclassing as well, so maybe that answers one of my questions above.

Streaming Delaunay Triangulation for Huge Datasets

Isenburg, Liu, Shewchuk and Snoeyink have an interesting paper on contructing Delaunay triangulations over huge datasets using a streaming technique.


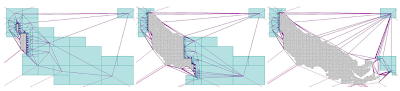
I'm quite interested in this, because here at Refractions I've just finished working on a project which involved computing a TIN for the province of B.C. using 500 million masspoints. After briefly flirting with the idea of computing a single seamless TIN, I ended up computing it in a piecewise fashion. This probably turned out to be a better approach for other reasons (such as the fact that we could easily parallelize the process). However, it would be very cool to be able to compute a seamless TIN for the entire province. And the approach in this paper sounds very effective - they quote a billion triangle in 48 minutes on a laptop!

It's also exciting to see the emergence of a whole new class of algorithms focussed on dealing with VLSD's (very large spatial datasets). As the same authors point out in another paper, paradoxically, advances in computing technology can make geospatial processing more difficult
because the rate of growth of dataset size far outstrips memory capacity.

Incidentally, these guys are a bit of a dream team for computational geometry algorithms. Shewchuck is the developer of Triangle, one of the best known programs for computing constrained 2D Delaunay triangulations (which is also AFAIK one of the few available systems to seriously address robustness issues - JTS of course being another one!) Snoeyink has done research in all kinds of different areas of CG, including interesting work in computing watershed boundaries on TINs using B.C. data.

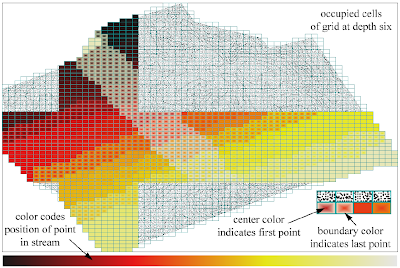
The paper also has a nice way of showing the spatial distribution of two related variables, using fill gradients:

Slow Forward - or back?

Here's an interesting take on the technological revolution by Gwynne Dyer (contrarian as always!). His point is that while life was dramatically transformed by numerous new technologies introduced between the 18th century and the 1950s, since then there's only really been one transformative technology, the computer (I guess he's discounting space travel since it's not generally available, or maybe because it's irrelevant?).

He has a good point, but I wonder whether he's ignoring quantitative effects of change. Sure, planes were around in the early 20th century, but they weren't allowing huge numbers of people to wash around the world in the way they do now. 9/11 would have been impossible in the 1920's, for instance. And maybe the steady improvments in speed of communication really will result in the so-called "inflection point".

But... in the end, he does mention what may turn out to be the most important quantitative effect of technological developments on humanity. His final point talks about the coming "... drastic changes in the climate that affect everything ...".

Engines of Logic

It seems only right that I put in a plug for the book Engines of Logic by the other, more famous Martin Davis. And here's an interesting article which reviews the book in particular reference to the occupational health hazards of being a mathematician. It's a good antidote to any regrets you might have about not being real smart.

Quote of the Day

If it wasn't for Alan Turing, I'd either be unemployed or working for the Nazis.

- unknown IT worker

The Vietnam of Computer Science?

I couldn't resist the analogy of this blog article, even if the author slightly overstates the case. Good summary of the history of the war, too.

Makes me feel like if I haven't served a tour in the Delta, at least I've done time at a forward fire base...

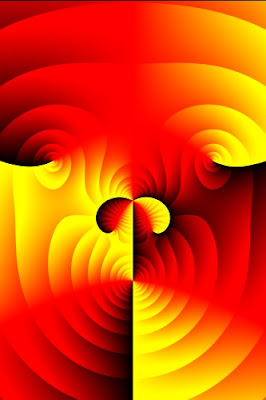
Complex Functions as Algorithmic Art

Hans Lundmark has an interesting page on visualizing complex functions. The idea is to map functions from f : C → C using position, hue, and saturation. The domain values of the function provide the (x, y) position. The function output value provides the hue and saturation; the hue is determined by the complex argument (angle), and the saturation is determined by the absolute value.

The output struck me as a nice example of algorithmic art. I whipped up my own version in Java to experiment, and to be able to produce high-resolution images for printing. Here's a couple of my images:

An example function from the paper ( f ( z ) = ( z − 2 )² ( z + 1 − 2i ) ( z + 2 + 2i ) / z³ )



^{"Wild Walrus"}

PreparedGeometry - efficient batch spatial operations for JTS

A common usage pattern for JTS spatial operations (in particular, predicates such as intersects and contains, and overlay operations such as intersection and union) involves the operation being invoked between a single target geometry and a batch of test geometries. For instance, this occurs in queries in a spatial database such as PostGIS, where each geometry in the driving table interacts with a set of nearby geometries via the required operation. By taking advantage of the fact that the target geometry does not change, it is possible to significantly reduce the overall execution cost of the operation. Information such as an index on the line segments in the target geometry can be computed once and cached for reuse with all of the test geometries.

In order for this to work, the calling code must be able to indicate that the operation is being invoked in a batch setting. The standard JTS Geometry API doesn't allow differentiating this case, so the new concept of PreparedGeometry has been developed. (This name intentionally echoes the concept of prepared statement in SQL API's, which implements the same strategy.) Creating a PreparedGeometry on a target Geometry enables precomputation of various data structures, which then allows subsequent operations to be evaluated with maximum efficiency.

In addition to caching, it is also possible to optimize the evaluation of spatial predicates. Optimization takes the form of short-circuiting predicate evaluation when certain situations are detected. While not all OGC spatial predicates are amenable to optimization, fortunately the most commonly usd predicates, intersects and contains, can be optimized significantly. Examples of situations which can be optimized are:

• For intersects, any intersection between line segments indicates a true result. If there is no intersection between any line segments of the operands, and the target geometry is polygonal, then one or more fast point-in-polygon tests can be performed to compute the result value.
• Since it provides more information than intersects, the contains predicate is more complex to optimize. In the case where the target geometry is polygonal, evaluation can be short-circuited when the test geometry has no line segment intersection. In this case, containment can be tested by an appropriate set of point-in-polygon tests. It is also possible to short-circuit in some specific cases where a proper intersection is detected between two line segments. Both of these situations can be tested efficiently.

The performance gains from using PreparedGeometry in real-world situations can be dramatic - up to 40 times improvement in speed. This functionality will appear in the next release of JTS, and hopefully will make its way into GEOS and PostGIS as well.

Flex VS Silverlight - another shot in the war

Another interesting post by Kurt Cagle on The Open-Sourcing of FLEX (no, I'm not paid to shill for Kurt - even if we do live in the same town). I've been wondering how the Flash/Silverlight war was going to evolve, but I'd missed this turn of the strategy. Kurt has some interesting points:

• Open Source is a weapon to gain market share
• Does this promote the slow death of SVG? And will Mozilla team up with Adobe to promote Flex? (If so, maybe this answers the question about how the OS community will provide a story to reply to Silverlight)
  
• Does OS-ing Flex enhance Adobe's ability to improve the technology with feedback from OS adopters?

The battle for the client UI is going to be very interesting to watch, and the outcome is going to affect the way we design applications for a long time to come. I'd give the edge to MS in this one (much as I hate to say it) except for one thing - will they sacrifice lock-in to the Windows platform in order to ensure dominance for their client platform? That's a hard one to call...

Where is XML going?

Kurt Cagle has an interesting post on "Where is XML going".

One of his bold predictions is that SQL databases (by which I think he means relational DBs) are going to plateau and slowly be replaced by XML-based DBs. I find that a fascinating possibility. Certainly the emergence of XQuery finally provides a decent query language for XML (and it's interesting to note that it draws from or at least parallels many SQL concepts).

One question I have is whether the XML information model is in fact more expressive than the relational model. It certainly seems so, since you can easily represent a table in XML, but the converse is not so simple. XML contains implicit information about hierarchy, which must be supplied in a relational model. It seems like there should be some sort of information content metric which could be used to determine which model is more powerful. Although, perhaps the human factors are in the end more important.

Also, to me it feels like XML suffers from too much concern with syntax (whereas relational is a pretty pure data model). There's also the cruft of elements versus attributes, processing instructions, etc. All of these complicate the XML model without bring a lot more data expressiveness. Perhaps simple use patterns will emerge and we'll all just get used to ignoring this stuff (but it seems to me that's been said about SOAP as well, and look how successful that's been...)

Do mountains exist?

I came across this provocatively-titled paper while web-surfing looking for information on ontology. It's a fun read, if you're into that kind of stuff. I don't think the paper really tackles its proposed thesis in a head-on way, but it does raise some interesting points about the philosophy of geospatial data, such as:

• What is the real definition of a mountain? Sure, we all know one when we see one - or do we? Go ahead - try and define this concept in a rigourous way...
• There is a long-standing schism between between feature-based and field-based views of natural phenomena. Both are useful, in different contexts. (This seems to me to echo the particle-wave duality of quantum mechanics - is there possibly some sort of fundamental dichotomy going on here?)
• Every so often this kind of debate surfaces in the geospatial world (a recent example is this thread on the GeoWeb blog). But we are as babes in the wood compared to philosophers, who have been debating this topic for at least 2000 years. Fortunately, it looks like the kindergarten of computer science is beginning to engage in a useful dialogue with the fusty temples of philosophy.
  

The ultimate Point-In-Polygon implementation

The classic stabbing line/ray-crossing point-in-polygon algorithm has been around for longer than computational geometry itself. (See William Franklin and SoftSurfer for background and description. ) The algorithm as usually published is short, effective and clever. But it does have some limitations:

1. It is implemented as an iteration over a data structure representing a sequence of line segments. This ties the algorithm to a fixed data structure, which leads to code duplication
   
2. It handles simple rings, but not fully general polygons (which may contain holes and/or multiple shells)
3. It does not detect the case where the query point lies on one of the segments in the polygon
4. It runs in O(n) time. This is reasonable for a single query point, but is not the most efficient way to perform many point queries against a single fixed polygon
5. It uses conventional floating-point arithmetic. This makes it non-robust (i.e. potentially incorrect for some inputs)
   

This predicate forms a key component of many spatial processing algorithms. In JTS it's used all over the place. The more places it's used, the more the above limitations have become apparent. Over time I've been slowly chipping away at removing them.

Most recently, I've revisited P-I-P in the course of some work on improving the performance of spatial predicates. And I think I've finally arrived at the ultimate Point-In-Polygon implementation. It removes all of the above limitations with the following design features:

1. It uses an incremental design, which frees the algorithm from being tied to any particular segment data structure
2. It handles all polygonal geometry types defined in JTS. (Implementing this was made much cleaner by the pleasant realization that the PIP algorithm really doesn't care where in a polygonal geometry the segments come from. The only thing that matters is the parity of the segment crossings. This holds true for any number of holes and shells.)
   
3. It detcts the point-on-segment case, and reports it via a trivalent return value (in the set {INTERIOR, BOUNDARY, EXTERIOR}).
4. It is straightforward to use with a spatial index on the segments of the polygon (such as STRtree or BinTree), thus providing O(log n) performance
5. Thanks to the RobustDeterminant class in JTS, the implementation is much more robust. (Due to some remaining floating-point arithmetic it may still not be 100% robust - but I hope to address that sometime as well.)
   

Even with all these changes, it's not much more complex than the original algorithm (at least, not given various supporting components which are already available in JTS.)

Coming soon to a JTS version near you...

Relations - the machine code for data?

In the rushing torrent of computer science, a few concepts stand like rocks which resist being swept away. One of the most familiar and useful is relational database technology. It took a relatively short time for this concept to be identified (in Codd's paper of 1970) and implemented commercially (around 1975, in IBM's System R, among others). Perhaps only 10 or 15 years elapsed between the earliest database systems and the emergence of commercially viable RDBMS . For over 30 years since then RDBMS's have stood the test of time and repelled all challengers to their central role in data management.

A recent and serious challenger was Object database technology. In the 1990's this area looked poised to ride the gathering wave of object-oriented programming and sweep aside the fusty old RDBMS technology. Since then, while the OO wave has swept far up the beach, the promise of ODBMS seems to have been left behind in the receding foam, never having been fully realized.

So why is this?

I think one reason is that the relational paradigm could be a fundamental data structure for information representation. In a sense, relations are the machine code of data modelling - they can be used to represent any required data model. Granted, relational models aren't alway elegant or efficient - but that simply confirms the metaphor. Moreover, their simplicity allows relational theory to be firmly grounded in mathematics and logic. (Of course, the relational hard-cores have been saying this for years - in some cases a bit too vociferously, IMHO. I'm just reluctantly coming round to think that they might be right.)

A further piece of evidence for this observation is that RDBMS vendors have a fine track record of being able to adapt the core paradigm to accomodate new technical ideas. Queuing, security models, data analytics, and of course even (to an extent) object-orientation are some of the areas which have been implemented quite reasonably in terms of an underlying relational model.

ODBMS's, in contrast, have never quite seemed to develop a truly compelling and general paradigm. The various OO query languages don't seem to have the expressive power of SQL, and Object data models seem to run up against thorny semantic issues sooner than relational ones do (such as schema evolution and inheritance modelling). Granted, implementing an object-based data model using relational technology doesn't actually solve any of these issues, but somehow the maturity of relational techniques and tools make them seem less painful.

Some people (myself included) have tended to see the rise of Object-Relational mapping technology as at best a temporary expedient, and at worst a string-and-baling-wire solution to cope with the OO-RDB impedance mismatch. Just give ODB's a few more years to mature, we hope, and we can do away with this inelegant hack! But if relational really is a fundamental concept, perhaps the quest for pure OO databases is misguided. Perhaps O-R mapping tools are the final goal, not just a stop-gap. They can be thought of as compilers for the data access layer (with all the opportunity for performance improvement and platform independence that the compilation paradigm provides).

This isn't to say that RDB technology has evolved as far as it needs to. I hope to see much more powerful querying capability, using concepts from the areas of logic and functional programming, machine reasoning and knowledge representation. All of these seem to be continuing to mature - I look forward to seeing them make the leap to practicality like OO did years ago.

Packed 1-dimensional R-Tree for Geometric Algorithms

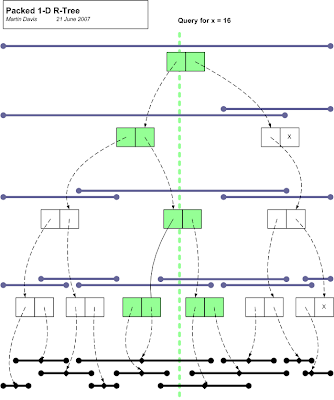
Some geometry algorithms depend on searching a fixed set of 1-dimensional intervals for the ones which contain a given value. An example is Point-In-Polygon testing using the stabbing line method. In cases where the algorithm needs to be run multiple times for different input values, the performance can be improved if a suitable data structure is used to increase the efficiency of search.

Here's an idea for an index which allows fast lookup of 1-dimensional intervals. It is basically a 1-dimensional R-tree, with a packing scheme which allows easy creation of the index for a fixed set of intervals. The index has the following charateristics:

• It indexes 1-dimensional intervals over some ordered set of values (for geometry, usually floating-point numbers)
• It indexes a static, pre-known set of items. Once built the index cannot be modified.
  
• Queries can be by either range or single value (stabbing queries), and return the set of all items which intersect the query value
• One optional parameter is the bucket size
  

The tree contains two types of nodes: leaf nodes, which contains the stored intervals (and any additional user-specific information), and interior nodes, which contain an interval and references to two child nodes which lie in that interval.

To build the tree:

• sort all the intervals to be indexed by their midpoint. These form the leaf nodes of the tree.
  
• Create new interior nodes for every adjacent pair of nodes, assigning the new node to have an interval which spans the intervals of its children. If there is only one child available, do not create a new node for it.
• Recursively repeat the previous step, until a single node is created. This is the root node of the tree.

Searching the tree is simple:

• traverse the tree in depth-first order, pruning branches which have intervals which do not intersect the query value.

A nice aspect of this data structure is that it is simple to build. It should be possible to implement the structure using two arrays, one for leaf nodes and one for interior nodes. This should provide a pretty efficient and straightforward implementation in C.

The interior node definition can easily be generalized to allow n intervals per node (the bucket size). Of course, there's a trade-off between increasing fan-out and decreasing selectivity. It's not obvious to me where the sweet spot is.

Really this is a 1-dimensional version of Leutenegger & Edgington's STR tree. JTS even contains an implementation of this, using the generalized STRtree classes already in JTS. The novelty here is the exploration of just how simple the implementation of this structure can be. A simple implementation should be faster to build and query, as well - this is a subject for some performance testing.

There are several (lots?) of other data structures for efficiently querying sets of intervals. The segment tree and interval tree are probably the most well-known. Both of these structures are more complex to understand and implement, I believe. In addition, I don't think that they are amenable to an implementation based solely on two simple arrays.

Presentations at FOSS4G 2007

I'm giving two talks at FOSS4G 2007, which is taking place here in Victoria in September. The abstracts are:

The JTS Topology Suite: Tools, Tips & Techniques

The JTS Topology Suite is one of the most widely used geometry libraries for Java. This talk will review the standard geometry methods in JTS, with an emphasis on their finer details. Some of the additional algorithms and components which the library provides will be discussed. Tips for improving performance and techniques for accomplishing various kinds of geometric processing tasks will be presented. The talk will conclude with an preview of some potential future developments for JTS.

Automatic watershed delineation using open source Java

The B.C. Corporate Watershed Base is a large-scale database of hydrographic information built using open source products. This talk discusses the development of an open source system for automated delineation of watershed boundaries based on CWB hydrography and a terrain model.


If previous years are anything to go by, this conference should be very informative and energizing. See you there!

History of JTS and GEOS

It seems a good thing to record the history and provenance of JTS and GEOS, for the following reasons:

• JTS and GEOS have attained a certain prominence in the open-source geospatial world. Sometimes comments are made which make assumptions about their goals and project structure which indicate a lack of knowledge about the true situation. Time to set the record straight!
• The legal attribution of code provenance bears little relationship to the true origin of the intellectual property incorporated in these projects. It seems only fair that the people who actually contributed to these projects have their participation recorded.
• As the designer/lead developer for these projects, I have the most knowledge about their origin and history.

JTS

JTS is the result of the fortuitous convergence of two situations. The first was that I had been working on spatial algorithms since the mid-90's. At that time I held a position in the BC Ministry of Forests, with a major focus being geomatics and spatial data management. While there I developed algorithms in C++ for polygonization and the beginnings of a polygon overlay algorithm. These were based on a simple spatial data model and included implementations of several fundamental computational geometric functions. A colleague, Brian Howden, was very encouraging in this work. Brian and I both felt that what the world really needed was a good spatial library, and this motivated me to start packaging my code as a reusable library. However, progress was slow and I did not feel like I had a clear idea of what such a library should look like. Moreover, library development in C++ was quite painful, since it requires such painstaking attention to details of memory management and code structure.

The second situation was my connection with Dr. Mark Sondheim, of the Geographic Data BC (GDBC) branch of the BC Ministry of Environment, Lands and Parks. I had known Mark since the early 90's, and had interacted with him on numerous occasions while I was working for the BC Government. Over the years we had many stimulating discussions about geospatial processing, and shared a similar interest in increasing the accessibility and formality of spatial data processing.

The JTS Topology Suite formally started life as a project conceived and initiated by Mark. The name and acronym were his idea, as was the concept of using the OGC Simple Features Specification as the basis for the API design. This latter idea was a key choice, since the SFS strikes a good balance between functionality and design complexity. Mark was confident that the SFS geometry model provided everything needed for most geospatial work, and time has proven him correct.

By 2000 I had moved to Vivid Solutions Inc. as a consultant, working primarily in Java and as much as possible on geospatial projects. While there I worked on a couple of spatial projects for GDBC which were Java based (most notably, a streaming parser for SAIF, a forerunner of GML developed by Mark Sondheim and others). I was also working on various projects which utilized my C++ spatial library (including some Java-based ones, necessitating the awkward and limiting use of JNI). Howver, there was never sufficient time or budget to contemplate re-implementing the C++ geometry library in Java (and, I have to admit, perhaps not the vision on my part that this would be as useful as it has turned out. In my defense, at that time Java was still proving itself as an efficient tool for development work).

Luckily, Mark did have the vision, and the access to funding. As a result, the JTS project was initiated in Fall 2000. The project goal was very clear: to develop a Java API which implemented the OGC Simple Features Specification. Given my experience and previous work, I suspect it was an easy choice to award the contract to Vivid Solutions. The project team consisted of myself as designer and lead developer, and Jonathan Aquino as a developer.

The project charter did not highlight the requirement for efficiency and robustness, since Mark wisely realized that these goals would have to be proven to be attainable during the course of the project. In hindsight the need for efficient performance should have been obvious; the need for robustness perhaps less so. (JTS is not exceptional in this area - a disappointly large percentage of published computational geometry algorithms fail to address this issue.) In any case, once the basic functionality was achieved, these two aspects emerged as much more important. Even today, they are still the most important issues in JTS development.

David Skea (at that time also with GDBC) contributed valuable direction and guidance. Most notably, it was his recommendation that an explicit precision model be provided, and he provided much insight about implementing robust spatial algorithms.

At the outset of the project it seemed that the main challenges were going to be designing the algorithms for spatial relationships and polygon overlay. Buffering was lurking in the background with an unknown level of difficulty. Mike Butler (the "father of SDE") had warned me that buffering would be a significant challenge, but since at that time he was still under NDA to ESRI, he did not provide me with any implementation advice. Later in the project when I tackled buffering I found out how right he was!

Development proceeded fairly quickly, with myself tackling API and algorithm design, and Jon working on I/O and implementations of structural methods. Jon also worked on the Unit Test facilities. David Skea contributed the core of the line segment intersection implementation, including the key development of deVillier's robust 2x2 determinant algorithm. Yao Cui of GDBC did good work on categorizing and defining test cases for the spatial predicates (which now appear as part of the JTS validation tests, a useful body of work in its own right).

In the middle of the project I realized that spatial visualization would be essential for designing and debugging spatial algorithms, and I also realized that Java2D and Swing would provide a great platform to build a visualization tool. This led to the development on the TestBuilder as an important component in the JTS toolkit. Jon and I shared development of the TestBuilder. This experience was very valuable in our subsequent development of JUMP.

JTS 1.0 was released in February 2002. The scheduling of this release was primarily motivated by contractual requirements. As soon as it was released I continued work on validation and buffer improvements. This resulted in the release of Version 1.1 in March 2002. At this point the contract with GDBC came to an end. I was encouraged by the success of the JTS development, and I made a personal commitment to continue to enhance JTS with better and more algorithms.

Subsequent releases of JTS have been motivated by my desire to see the library grow, by bug reports and suggestions from clients and users, and occasionally by directly-funded work (notably, work I carried out in 2006 on improving the robustness of polygon overlay). JTS has moved beyond the basic SFS by providing functionality such as polygonization, simplification, linear referencing, affine transformations, and a wide variety of structural functions. One day perhaps it will even provide a true topology API !

It's fair to say that JTS has been wildly successful in fulfilling the goal of providing a full-featured, robust, efficient library of spatial operations. It is being used in numerous spatial applications, notably:

• JUMP (and derived projects)
• GeoTools (and derived projects),
• the BC Goverment/Moxie Media Internet Mapping Framework

There are many, many other applications and projects using JTS as well.

GEOS

In 2003 PostGIS was emerging as a serious and useful spatial database. However, there was one thing it sorely lacked - a complete set of spatial functions. Paul Ramsey and I strategized that the functions in JTS were an excellent basis for filling this gap. The big catch was that PostGIS required a pure C implementation. Never being one to shy away from thinking big, Paul proposed that we port JTS to C++. At that time Dave Blasby was still involved with PostGIS development, and it was he who came up with the name of Geometry Engine (Open Source) - GEOS.

Initially the GEOS project was funded jointly by Refractions Research Inc. and Vivid Solutions, with myself as Technical Advisor (and to a limited extent Architect), and a University of Victoria Master's student named Yury Bychov as developer and designer. Since I was busy on other projects, and in any case would not claim to be an expert in the byzantine area of C++ code design, the plan was that Yury would provide any extra design needed to accomodate differences between Java and C++, and I would advise as much as possible on the purely functional design of the API.

We knew that C++'s lacks of automated memory management would be a major challenge, and I also expected that its much more flexible (some would say baroque) features for code organization (e.g. templates, namespaces) would require some careful thought. I had no idea that the porting process would be quite so painful and prolonged, however. In the end it took longer to port JTS to C++ than it did to develop the entirety of JTS up to Version 1.1! [This is the main reason why my strategy for designing and implementing spatial algorithms remains focussed on Java as the development language, with the GEOS port happening only after the algorithms are relatively stable and well-understood. In my opinion C++ is less effective for algorithm design since it requires too much brainpower devoted to irrelevant issues.]

Since its initial release GEOS has been incorporated in PostGIS, of course, and also in MapGuide and apparently in at least a few other C-based projects. GEOS code has been incorporated by Safe Software in their FME product. MapServer has announced plans to incorporate GEOS in their codebase (the status of this is unknown to me). Frank Warmerdam's OGR project I believe uses GEOS.

GEOS also continues to undergo development, both in the orginal mode of direct ports of JTS code, and also to a certain extent with independent functionality (primarily involving making it better adapted to C++ programming styles).

Martin Davis, May 2007

Monotone Chains: the unknown technique

When I was originally developing JTS, I spent quite of bit of time thinking about and researching techniques for efficiently computing arrangements (intersections) of sets of linestrings. There's a relatively large body of literature on this subject, as you might expect since it is such a key aspect of many geometric algorithms. As usual, however, much of this literature is fairly academic in nature, and usually doesn't address some of the more mundane issues which an implementor has to deal with.

One issue that crops up with intersecting sets of linestrings is that there is a tension between increasing performance and decreasing memory use. The fastest way should be to indexing individual line segments. However, this implies creating a new memory structure for each line segment, which can be both time and memory intensive. The most memory-effective structure is of course to leave the original linestrings undivided, but this does not provide good performance.

It seemed to me that there must be an intermediate between these two extremes. After some thought I came up with the idea that I called "monotone chains". A monotone chain is a string of line segments which are monotonic in both X and Y directions. This structure has some nice properties:

• Monotone chains cannot self-intersect
• Two monotone chains intersect in at most one connected set of line segments.
• The envelopes of any two subsequences of a monotone chain are interior-disjoint. This means that the envelopes of successive bisections of the chain form a "pyramid" of envelopes. In turn, this allows comparing two chains for intersection can be carried out using a binary search technique using the two envelope pyramids.
  

In addition, splitting linear geometry into monotone chains is a good heuristic for partitioning the geometry. Often digitized linework representing natural features contains quite long sequences of segments which are monotone (since the linework follows natural curved features.

I was pretty pleased with my "discovery", and used it to good effect in JTS. For quite a while I was unaware of any prior use of this technique, but recently I came across a reference to a paper by Warren Burton in 1977 which apparently discusses this technique. I was led to this by the paper on Whirlpool by Nick Chrisman et al., which used this technique under the name "monotone sections".

It doesn't come as too much of a surprise that such a simple and useful technique has been used before, but what I do find a bit surprising is how little this technique is discussed in computational geometry literature. I presume the reason for this is that the technique is too simple to be of continuing interest to academics, while it is too special-purpose to be worth presenting to students. There's a dearth of computational geometry literature directed at the true practitioner - which probably indicates how few practitioners there are!

References

Burton, Warren 1977: Representation of many-sided polygons and polygonal lines for rapid processing, Communications ACM, vol. 20, no.3.

Chrisman, N.R., Dougenik, J.A. and White, D. 1992: Lessons for the design of polygon overlay processing from the Odyssey Whirlpool algorithm, Proc. 5th Int. Symp. on Spatial Data Handling, 2, 401-410.

Quirks of the "Contains" Spatial Predicate

One of the most useful OGC standards is their specification of the Dimensionally-Extended 9 Intersection Model for spatial relationships. (To give credit where is it due, this was originally developed by Egenhofer, Clementini and others). In its most general form this model is quite complex, so to make it usable for mortal programmers, a set of commonly-useful "named predicates" have been specified. These include obvious relationships such as intersects, disjoint, touches, equals, and contains.

But are they really so obvious? In fact not - several of them have subtle aspects to their definition which are contrary to intuition.

In particular, "contains" (and its converse "within") has an aspect of its definition which may produce unexpected behaviour. This quirk can be expressed as "Polygons do not contain their boundary". More precisely, the definition of contains is:

Geometry A contains Geometry B iff no points of B lie in the exterior of A, and at least one point of the interior of B lies in the interior of A

That last clause causes the trap - because of it, a LineString which is completely contained in the boundary of a Polygon is not considered to be contained in that Polygon!

This behaviour could easily trip up someone who is simply trying to find all LineStrings which have no points outside a given Polygon. In fact, this is probably the most common usage of contains. For this reason it's useful to define another predicate called covers, which has the intuitively expected semantics:

Geometry A covers Geometry B iff no points of B lie in the exterior of A

Its converse coveredBy is also useful as well. It's a bit of a mystery why OGC did not define this predicate. In any case, Oracle Spatial does provide this predicate. I have added it to JTS as well.

There's a further bonus to defining the covers predicate. It is much easier to optimize the common use case:

covers(Rectangle, Geometry)

All that is necessary to determine this condition is to perform a simple bounding box comparison. This is not possible with contains, because even if the bounding box of Geometry is covered by the Rectangle, a further expensive operation is required to test if the Geometry lies wholly in the boundary of the Rectangle (in which case the predicate fails).

Covers "simplifies" the defintion of contains by making it more general (inclusive). There's another possibility as well, which is to simplify in the direction of being less inclusive. This would produce a predicate which might be called containsProperly, with the definition:

Geometry A containsProperly Geometry B iff all points of B lie in the interior of A

Interestingly, some recent work I'm doing indicates that this predicate might play a very useful role - but that's a story for another post.


References

DE-9IM: Clementini, Eliseo, Di Felice, and van Osstrom; "A Small Set of Formal Topological Relationships Suitable for End-User Interaction," D. Abel and B.C. Ooi (Ed.), Advances in Spatial Database—Third International Symposium. SSD '93. LNCS 692. Pp. 277-295.

9 Intersection model: M. J. Egenhofer and J. Herring; "Categorizing binary topological relationships between regions, lines, and points in geographic databases," Tech. Report, Department of Surveying Engineering, University of Maine, Orono, ME 1991.

GeoTec 2007 presentation on Automated Watershed Boundary Generation

I'm giving a talk at GeoTec 2007 in Calgary entitled "WaterBuG: An Automated Generator for Watershed Boundaries". This covers a project I've been working on for the last year-and-a-half. It's a very cool application of complex large-scale geo-processing, using a whole assortment of nifty geometric structures and algorithms such as:

• quad-edge subdivisions for modelling
  
• Triangular Irregular Networks (Delaunay triangulations)Delaunay triangulation refinement
• Medial axis refinement
• Surface modelling with a TIN
  
• Surface hydrological flow modelling over a TIN
• Flood filling
• Depth- and breadth-first Graph traversal
  
• Topology-preserving Linestring smoothing
• Discrepancy detection
  

Here's a couple of screenshots from the talk - I'll post the full presentation sometime soon, somewhere...