Better/Faster ST_PointOnSurface for PostGIS

And now for the final chapter in the saga of improving InteriorPoint / PointOnSurface.  For those who missed the first two episodes, the series began with a new approach for the venerable JTS Geometry.interiorPoint() for polygons algorithm.  Episode 2 travelled deep into the wilds of C++ with a port to GEOS.  The series finale shows how this results in greatly improved performance of PostGIS ST_PointOnSurface.

The BC Voting Area dataset is a convenient test case, since it has lots of large polygons (shown here with interior points computed).

The query is about as simple as it gets:

   select ST_PointOnSurface(geom) from ebc.voting_area;

Here's the query timings comparison, using the improved GEOS code and the previous implementation:

Data size	Time	Time OLD	Improvement	Time ST_Centroid
5,658 polygons (2,171,676 vertices)	341 ms	4,613 ms	x 13	369 ms

As expected, there is a dramatic improvement in performance.  The improved ST_PointOnSurface runs 13 times faster than the old code.  And it's now as fast as ST_Centroid.  It's also more robust and tolerant of invalid input (although this test doesn't show it).

This should show up in PostGIS in the fall release (PostGIS 3 / GEOS 3.8).

On to the next improvement... (and also gotta update the docs and the tutorial!)

Better/Faster Interior Point for Polygons - now in GEOS

As a gentle introduction to GEOS development I took on the task of porting the recent improvements to the JTS InteriorPointArea algorithm.   This is a fairly small chunk o'code, but it touches most of the aspects of GEOS development process: build chain, debugging, unit tests, and infra (source control and build farm).  It also has the advantage that the JTS code was still hot off the keyboard and (almost) unreleased, so it was a chance to see if any cross-fertilization would blossom from working on the two projects jointly.

Skipping lightly over the details of my (somewhat painful) GEOS learning curve, I'm delighted to say that the code has landed in master and is basking in the green glow from the build bot badges.

And now the whole point of the exercise: how much better is the new code in GEOS? 

It exhibits the expected improvement in robustness, since a GEOS test which actually depended on a thrown TopologyException (due to the now-removed call to Geometry::intersection() ) had to be modified to handle a successful return.

Most importantly, there is a dramatic improvement in performance.  Here's some numbers from running the GEOS InteriorPointArea performance test:

Data size	Time	Time OLD	Improvement	Time Centroid
100	.8 ms	86 ms	x 100	1 ms
1000	6 ms	144 ms	x 24	12 ms
10,000	55 ms	672 ms	x 12	107 ms
100,000	508 ms	6,714 ms	x 13	961 ms
1,000,000	5,143 ms	73,737 ms	x 14	11,162 ms

Some observations:

• The performance test uses synthetic data (sine stars).  Real-world datasets are likely to show significantly better times ( 80x better in some cases, based on JTS timings)
• The largest improvement is for small geometries, which is nice since these are more common
• InteriorPoint is now actually faster than the Centroid computation.  This is also good news, since users were often tempted to try and use centroids instead of interior points, despite the known issues.

Future Work

Running the identical performance test in JTS is still faster, by roughly 5x.  This may be due to the advantages of JIT compilation and memory management.  It may also indicate there is room for improvement by making GEOS smarter about data handling.

Better and Faster Interior Point for Polygons in JTS/GEOS

A humble workhorse of geospatial processing is the ability to compute a point which is guaranteed to lie in the interior of a polygon.  In the OGC Simple Features for SQL specification (and hence in PostGIS) this is known as ST_PointOnSurface.  In JTS/GEOS it is called getInteriorPoint, for historical reasons [1].

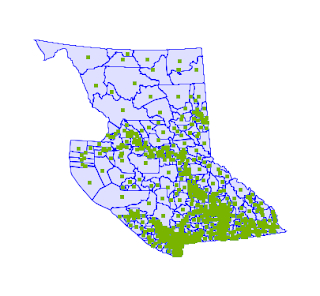
Interior points for country boundaries

There are some important use cases for this capability:

• Constructing a "proxy point" for a polygon to use in drill-down spatial query.  This has all kinds of applications:
• recovering attribution after polygon coverage generalization
• determining parentage during polygon overlay
• faster and more robust spatial join between polygonal datasets
• Cartographic rendering including:
• Creating leader lines
• Placing labels for polygons (for which it is a quick solution but not necessarily a quality one.  More on this in a later post)

There is a variety of ways that have been proposed to compute interior points: triangulation, sampling via random or grid points, medial axis transform, etc.  These all involve trade-offs between location quality and performance [2].  JTS uses an approach which optimizes performance, by using a simple scan-line algorithm:

JTS Scan-Line Interior Point Algorithm

1. Determine a Y-ordinate which is distinct to every polygon vertex Y-ordinate and close to the centre of the vertical extent
2. Draw a scan line across the polygon and determine the segments of intersection
3. Choose the interior point as the midpoint of the widest intersection segment

Locating a polygon interior point along a scan-line

The current code has been in the JTS codebase since the release of the very first version back in 2001.  It is elegantly simple, but is quite non-optimal, since it uses the overlay intersection algorithm.  This is overkill for the computation of the scan-line intersection segments.  It also has a couple of serious drawbacks: slow performance, and the requirement that the input polygon be valid.  These are not just theoretical concerns.  They have been noticed in the user community, and have caused client projects to have to resort to awkward workarounds.  It's even documented as a known limitation in PostGIS.

Thanks to Crunchy Data recognizing the importance of geospatial, we've been able to look into fixing this.  It turns out that a relatively simple change makes a big improvement.  The scan-line intersections can be computed via a linear-time scan of the polygon edges.  This works even for invalid input (except for a few pathological situations).

Interior points of invalid polygons

(LH invalid polygon shows suboptimal point placement)

Best of all, it's much faster - providing performance comparable to the (less useful) centroid computation.  The performance results speak for themselves:

Dataset	# polys	# points	Time	Prev time	Improvement
World countries	244	366,951	25 ms	686 ms	x 27
Land Cover	64,090	366,951	78 ms	6.35 s	x 81

This has been committed to JTS.  It will be ported to GEOS soon, and from there should show up in PostGIS (and other downstream projects like QGIS, Shapely, GDAL, etc etc).

More Ideas

Some further improvements that could be investigated:

• Use the centroid to provide the Y-ordinate.  This is probably better in some situations, and worse in others.  But perhaps there's a fast way to choose the best one?
• Use multiple scan-lines (both vertical and horizontal)
• Provide better handling of short/zero-width scan-line intersections
• Support clipping the interior point to a rectangle.  This would provide better results for cartographic labelling

---

[1] JTS was based on the original OGC SFS specification (version 1.1).  The spec actually does include a method Surface.pointOnSurface.  The reason for the different choice of name is lost to time, but possibly the reasoning was that the JTS function is more general, since it handles all types of geometry.  (One of the design principles of JTS is Geometric Uniformity, AKA No Surprises.  Wherever possible spatial operations are generalized to apply to all geometric types. There is almost always a sensible generalization that can be defined, and it's often quite useful.)

[1a] Also, the acronym IPA is much better than the one for PointOnSurface.

[2] Apparently Oracle has decided to provide blazingly fast performance by simply returning a point on the boundary of the polygon.  Thus proving the maxim that for every problem there is an solution which is simple, fast, and dead wrong.

Joining Crunchy Data to work on PostGIS

I'm happy to announce that I am taking a position with Crunchy Data as a Senior Geospatial Engineer.  I'm working alongside fellow Victorian geospatial maven extraordinaire Paul Ramsey, as the core of a proposed Geospatial Data Centre of Excellence.

Our mission statement is simple:  make PostGIS bigger, better, faster!

• Bigger - more spatial algorithms and functions
• Better - enhance existing functionality to make it easier to use, more powerful, and more robust
• Faster - keep looking for algorithmic optimizations and ways to use the power of Postgres to make spatial processing faster

A lot of this work will involve enhancements to the core GEOS geometry library.  Part of the goal is to keep JTS and GEOS aligned, so this should produce a nice boost to JTS as well.

Having been lurking in the background for many years now, I'm stoked to be (finally) able to work directly on PostGIS.  And I'm excited to be part of the Crunchy team. They have some of the leading Postgres experts in-house, so I'm expecting that it will be a great learning experience.  And their client list promises to expose us to some fascinating large-scale use cases for spatial data processing, which can only be good for the power and robustness of PostGIS.

I'm also looking forward to re-engaging with the geospatial open source community, and learning more about the (even bigger) open source Postgres community.  Great things lie ahead!