A great article on the emerging SMAQ stack for big data.
I wonder if PIG does spatial?
Why Organizations Need Expert Generalists
14 hours ago
Because the shortest distance between two thoughts is a straight line
1,"Goroka","Goroka","Papua New Guinea","GKA","AYGA",-6.081689,145.391881,5282,10,"U"
2,"Madang","Madang","Papua New Guinea","MAG","AYMD",-5.207083,145.7887,20,10,"U"
3,"Mount Hagen","Mount Hagen","Papua New Guinea","HGU","AYMH",-5.826789,144.295861,5388,10,"U"
...
0B,1542,AGP,1230,BBU,1650,,0,738
0B,1542,ARW,1647,BBU,1650,,0,340
0B,1542,BBU,1650,AGP,1230,,0,738
...
28,"Bagotville","Canada",48.330555,-70.996391,146,"Montreal","Canada",45.470556,-73.740833
29,"Baker Lake","Canada",64.298889,-96.077778,132,"Rankin Inlet","Canada",62.81139,-92.115833
30,"Campbell River","Canada",49.950832,-125.270833,119,"Comox","Canada",49.710833,-124.886667
30,"Campbell River","Canada",49.950832,-125.270833,156,"Vancouver","Canada",49.193889,-123.184444
...
CSVReader troute hasColNames: file: "routeLine2.csv";
trte = select fromCity, toCity,
Val.toDouble(fromLon) fromLon, Val.toDouble(fromLat) fromLat,
Val.toDouble(toLon) toLon, Val.toDouble(toLat) toLat
from troute;
tlines = select fromCity, toCity, line, len
with {
line = Geodetic.split180(Geodetic.arc(fromLon, fromLat, toLon, toLat, 2));
len = Geom.length(line);
}
from trte order by len desc;
tplot = select line,
Color.interpolate("f0fff0", "00c077", "004020", len / 200.0 ) lineColor,
0.4 lineWidth
from tlines;
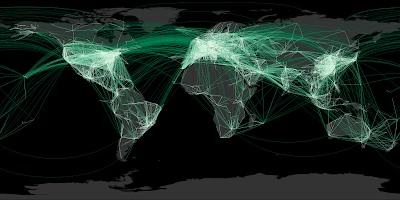
//----- Plot world landmasses for context
ShapefileReader tworld file: "world.shp";
tworldLine = select GEOMETRY, "22222277" lineColor from tworld;
tworldFill = select GEOMETRY, "333333" fillColor from tworld;
width = 2000;
Plot width: width height: width / 2
extent: LINESTRING(-180 -90, 180 90)
data: tworldFill
data: tplot
data: tworldLine
file: "routes.png";
BufferParameters bufParams = new BufferParameters();
bufParams.setSingleSided(true);
return BufferOp.bufferOp(geom, distance, bufParams);
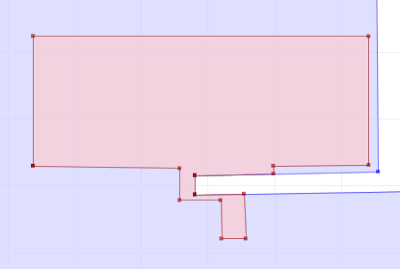
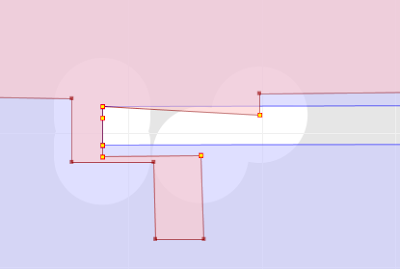
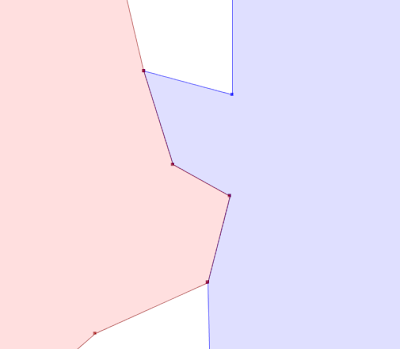
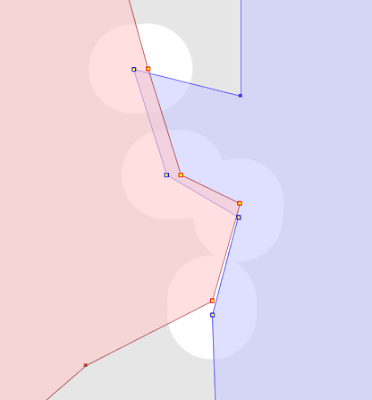
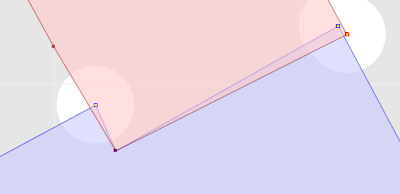
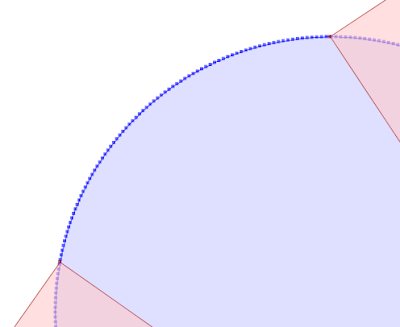
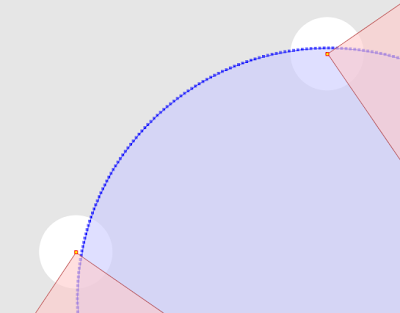
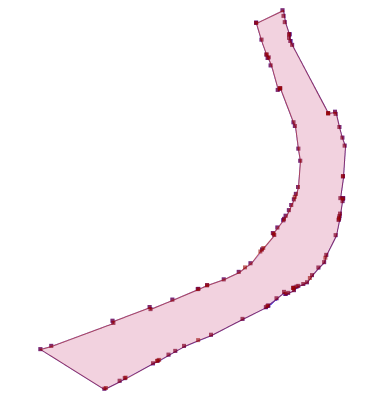
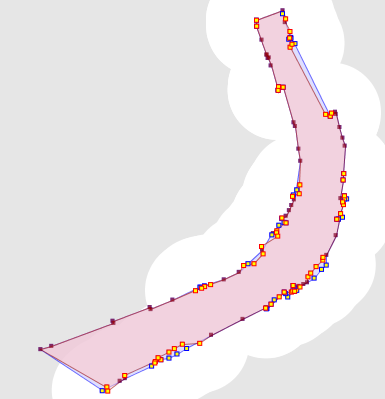
 Another alternative is a painstaking manual inspection of the coordinates of each vertex and segment (which by the way is straightforward in the TestBuilder and OpenJUMP, but can be difficult in other tools). But it's hard to convert the coordinate numbers into a mental image of the situation. And it's essentially impossible to do mentally if a vertex is near a non-rectilinear (slanted) line - in this case it's necessary to evaluate a complex mathematical algorithm to to determine the relative orientation of the vertex and line.
Another alternative is a painstaking manual inspection of the coordinates of each vertex and segment (which by the way is straightforward in the TestBuilder and OpenJUMP, but can be difficult in other tools). But it's hard to convert the coordinate numbers into a mental image of the situation. And it's essentially impossible to do mentally if a vertex is near a non-rectilinear (slanted) line - in this case it's necessary to evaluate a complex mathematical algorithm to to determine the relative orientation of the vertex and line.

public static boolean isInCircleDDSlow(
Coordinate a, Coordinate b, Coordinate c,
Coordinate p) {
DD px = DD.valueOf(p.x);
DD py = DD.valueOf(p.y);
DD ax = DD.valueOf(a.x);
DD ay = DD.valueOf(a.y);
DD bx = DD.valueOf(b.x);
DD by = DD.valueOf(b.y);
DD cx = DD.valueOf(c.x);
DD cy = DD.valueOf(c.y);
DD aTerm = (ax.multiply(ax).add(ay.multiply(ay)))
.multiply(triAreaDDSlow(bx, by, cx, cy, px, py));
DD bTerm = (bx.multiply(bx).add(by.multiply(by)))
.multiply(triAreaDDSlow(ax, ay, cx, cy, px, py));
DD cTerm = (cx.multiply(cx).add(cy.multiply(cy)))
.multiply(triAreaDDSlow(ax, ay, bx, by, px, py));
DD pTerm = (px.multiply(px).add(py.multiply(py)))
.multiply(triAreaDDSlow(ax, ay, bx, by, cx, cy));
DD sum = aTerm.subtract(bTerm).add(cTerm).subtract(pTerm);
boolean isInCircle = sum.doubleValue() > 0;
return isInCircle;
}
public static boolean isInCircleDDFast(
Coordinate a, Coordinate b, Coordinate c,
Coordinate p) {
DD aTerm = (DD.sqr(a.x).selfAdd(DD.sqr(a.y)))
.selfMultiply(triAreaDDFast(b, c, p));
DD bTerm = (DD.sqr(b.x).selfAdd(DD.sqr(b.y)))
.selfMultiply(triAreaDDFast(a, c, p));
DD cTerm = (DD.sqr(c.x).selfAdd(DD.sqr(c.y)))
.selfMultiply(triAreaDDFast(a, b, p));
DD pTerm = (DD.sqr(p.x).selfAdd(DD.sqr(p.y)))
.selfMultiply(triAreaDDFast(a, b, c));
DD sum = aTerm.selfSubtract(bTerm).selfAdd(cTerm).selfSubtract(pTerm);
boolean isInCircle = sum.doubleValue() > 0;
return isInCircle;
}
| # pts | DP | DD-self | DD |
|---|---|---|---|
| 1,000 | 30 | 47 | 80 |
| 10,000 | 334 | 782 | 984 |
| 10,000 | 7953 | 12578 | 16000 |

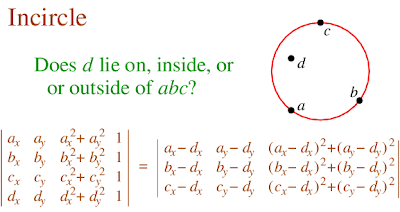
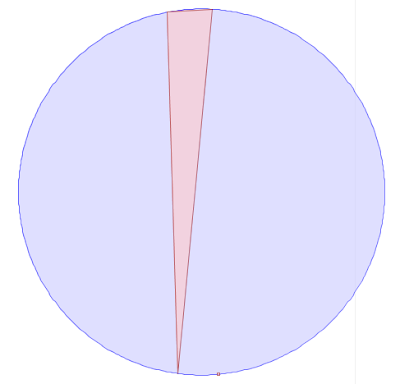
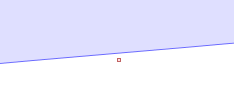 However, evaluating the inCircle predicate determinant using double-precision computes InCircle()=TRUE. This is because the large magnitude of the ordinate values relative to the size of the triangle causes the significant information to be lost in the roundoff error. The effect of this error propagates through the Delaunay algorithm. Ultimately this results in a convergence failure which is detected and reported.
However, evaluating the inCircle predicate determinant using double-precision computes InCircle()=TRUE. This is because the large magnitude of the ordinate values relative to the size of the triangle causes the significant information to be lost in the roundoff error. The effect of this error propagates through the Delaunay algorithm. Ultimately this results in a convergence failure which is detected and reported.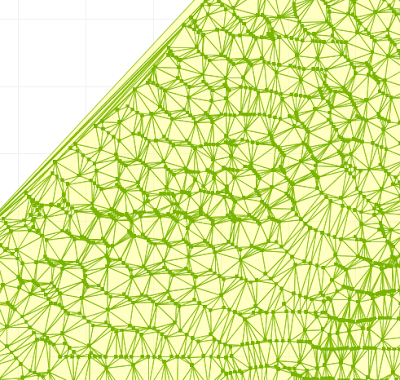


 Next idea: use square cells, but add a "gutter" between each cell. No points are created in the gutter, ensuring that points cannot be closer than the gutter width. In this image the gutter width is 30% of the overall cell width.
Next idea: use square cells, but add a "gutter" between each cell. No points are created in the gutter, ensuring that points cannot be closer than the gutter width. In this image the gutter width is 30% of the overall cell width.
 Maybe's there's still improvements that can be made.... It would be nice to avoid the grid effect, and also to reduce the use of a gutter (which skews the density of the distribution).
Maybe's there's still improvements that can be made.... It would be nice to avoid the grid effect, and also to reduce the use of a gutter (which skews the density of the distribution).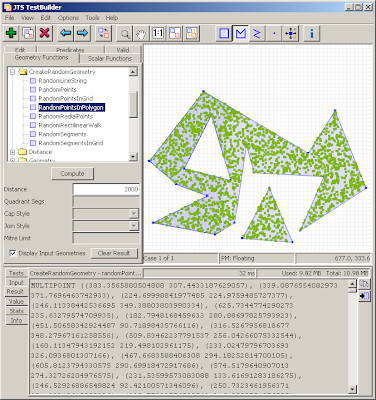

select ID, GEOM from T1 as t
inner join
HATBOX_MBR_INTERSECTS_ENV('PUBLIC','T1',145.05,145.25,-37.25,-37.05) as i
on t.ID = i.HATBOX_JOIN_ID
