The OGC Simple Features specification implemented by JTS has strict rules about what constitutes a valid polygonal geometry. These include:
- Polygon rings must be simple; i.e. they may not touch or cross themselves
- MultiPolygon elements may not overlap or touch at more than a finite number of points (i.e they may not intersect along an edge)
These rules were chosen for good reason. They ensure that OGC-valid polygonal geometry is the simplest possible representation of an enclosed area. This greatly simplifies the evaluation of most operations on polygonal geometry, which leads to improved performance. JTS operations generally require input which is valid according to OGC rules. And they always (with some rare exceptions) emit result geometry which is OGC-valid.
But data in the wild is often not this well-behaved. This creates the need to "clean" or "make valid" polygonal geometry in order to carry out operations on it. Shortly after JTS was first released we discovered a useful trick: constructing a zero-width buffer via geom.buffer(0) converts an invalid polygonal geometry into a valid one. It can also be used as a simple way of converting "inverted" polygon topology (ESRI-style) into valid OGC topology. The reason this works is that the buffer algorithm inherently has to handle overlaps and self-intersections since they often occur during the generation of raw buffer offset curves. The algorithm nodes self-intersections, merges overlaps, and creates new polygons or holes if necessary.
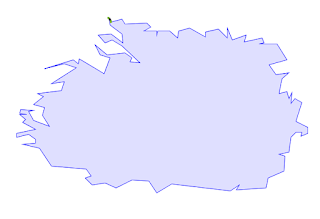
A polygon with many invalidities: overlap, self-touch in point and line, and a "bow-tie".
The polygon fixed by using buffer(0).
Note that the bow-tie portion on the right is considered to lie in the exterior of the polygon due to ring orientation, and thus is removed.
In the 20 years since the release of JTS (and its derivative
GEOS) this trick has passed into the lore of open-source spatial data processing. It has become a recommended technique for fixing invalid polygonal geometry in numerous projects, such as
PostGIS,
Shapely,
RGeo,
GeoTools,
R-sf and
QGIS. It's also used internally in JTS, in algorithms such as DouglasPeuckerSimplifier, VWSimplifier, and Densifier which might otherwise produce invalid polygonal results.
BUT - there's a nasty little surprise lying in wait for users of
buffer(0)!
It doesn't always work. It turns out that the buffer algorithm has a serious flaw: in some situations involving invalid "bow-tie" topology it will discard a large part of the input geometry. This has been reported in quite a few issues (
here and
here in JTS, and also in GEOS and Shapely).
Result of running DouglasPeuckerSimplifier on a polygon with a bow-tie. (See issue)
Close-up of the result - clearly undesirable.
The problem occurs because the buffer algorithm computes the orientation of rings in order to build the buffer offset curve (in the case of a zero-width buffer this is just the original ring linework). Currently the
Orientation.isCCW test is used to do this. This uses an efficient algorithm that determines ring orientation by checking the line segments incident on the uppermost vertex of the ring (see
Wikipedia for an explanation of why this works.) For a
valid ring (where the linework does not cross itself) this works perfectly. However, in a
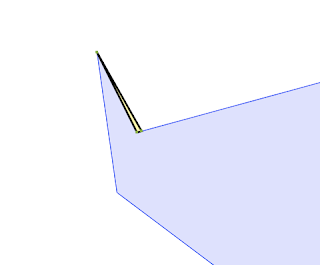
invalid self-crossing ring (sometimes called a "bow-tie" or "figure-8") a choice must be made about which lobe is assigned to be the "interior". The upper-vertex approach always picks the top lobe. If that happens to be very small, the larger part of the ring is considered "exterior" and hence is removed by buffering.
A bow-tie polygon where buffer makes the evidently wrong choice for interior.
The problem occurs for non-zero buffer distances as well.
This problem has limped along for many years now, never being quite enough of a pain point to motivate the effort needed to find a fix (or to fund one!). And to be honest, the buffer code is some of the most complicated and delicate in JTS, and I was concerned about wading into it to add what seemed poised to be a fiddly correction.
But recently there has been renewed interest in providing a Make-Valid capability for JTS. This inspired me to revisit the usage of buffer(0), and think more deeply about ring orientation and its role in determining valid polygonal topology. And this led to discovering a surprisingly simple solution for the buffer issue.
The fix is to use an orientation test which takes into account the entire ring. This is provided by the Signed-Area Orientation test, implemented in Orientation.isCCWArea using the Shoelace Formula. This effectively determines orientation based on the largest area enclosed by the ring. This corresponds more closely to user expectation based on visual assessment. It also minimizes the change in area and (usually) extent.
And indeed it works:
It fixes the simplification issue nicely:
The fix consists of about 4 lines of actual code. To paraphrase a great orator, never in the history of JTS has so much benefit been given to so many by so few lines of code. Now buffer(0) can be recommended unreservedly as an effective, performant way to fix polygonal geometry. And all those helpful documentation pages can drop any qualifications they might have.
As usual, this fix will soon show up in GEOS, and from there in PostGIS and other downstream projects.
This isn't the end of the story. There are times when the effect of buffer(0) is not what is desired for fixing polygon topology. This is discussed nicely in this blog post. The ongoing research into Make Valid will explore alternatives and how to provide an API for them.