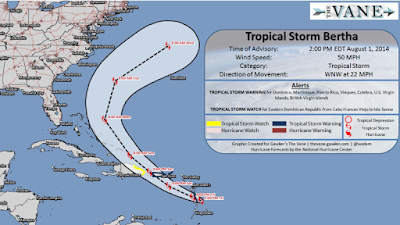
One way to generalize the buffer concept is to allow the buffer distance to vary along the geometry. As often the case with geospatial concepts this construction has a few different names, including tapered buffer, cone buffer, varying buffer, and variable-distance buffer. The classic use case for variable-distance buffers is generating polygons for the "cone of uncertainty" along predicted hurricane tracks:
Another use case is depicting rivers showing the width of reaches along the river course.
I took a crack at prototyping "variable width buffers" a few years ago, in the JTS Lab. Recently there were a couple of GIS StackExchange posts looking for this functionality in PostGIS and Shapely They were good motivation to buff up the prototype and move it into JTS core. But I was dismayed to realize that the output had some serious deficiencies, due to an overly-simplistic algorithm. The idea in the Lab code was appealingly simple: compute buffer circles around each line vertex at the specified distance, and union (merge) them with trapezoids computed around the connecting line segment. But this produced ugly discontinuities for large deltas in buffer distances.
For such a seemingly simple concept there is surprisingly little prior art to be found. Even the GIS That Shall Not Be Named does not seem to provide a native variable buffer function (although recently I found a couple of user contribs which do, to some extent). There's an implementation in QGIS - but since it seems to be based on the original problematic JTS code that didn't really help. So I had the fun of coding it up from scratch.
The problem with the original code is that it should have used the outer tangent lines to the buffer circles at each vertex. Wikipedia has a good discussion of this construction. Even better, it provides an elegant mathematical algorithm, which worked perfectly when coded up.
The construction computes a single tangent segment. The opposite segment is simply the reflection in the line between the circle centres. The geometric math to handle this is now provided for reuse as LineSegment.reflect(). Finally, it is notoriously tricky to produce buffer curves with high quality in the fine details. In this case, generating the line segment buffer caps required care to avoid creating out-of-phase vertices, which would produce a "bumpy" result when merged.
This is now available in JTS as the VariableBuffer class. In addition to the general-purpose API which allows specifying a distance at each vertex, it provides a couple of simpler functions which accept a start and end distance; and a start, middle and end distance. The first is an easy way to produce the classic cone of uncertainty. The latter is useful for buffering rings, or just creating interesting shapes.
The next step is to port this to GEOS. Then it can be exposed in PostGIS and all the other downstream projects like Shapely and R-SF, and maybe even QGIS.
Future Work
There's some enhancements that could be made:
- Some or all of the buffer end cap and join styles provided by the classic buffer operation could be supported, as well as the ability to set the quadrant segment count
- Variable buffering of polygons and multigeometries is straightforward to add.
- It might be possible to allow different distances for each side of the input line (although it may be tricky to get the joins right)
- The approach of using union to merge the individual segment buffers works well. But it would improve performance to feed the entire generated variable buffer curve directly into the existing buffer generation code
More experimentally, variable buffering might provide a way to construct a decent approximation to a true geodetic buffer. The vertex distances would be computed using true geodetic distance. There might be some complications around long line segments, but perhaps these can be finessed (e.g. by densification).