This Delaunay implementation arose out of the work I did on automated watershed extraction using a system called WaterBuG a while back. It's taken a while to make its way into JTS because there's quite a bit of work involved in turning a codebase targeted at a very specific project into a clean, user-friendly API. Not to mention writing documentation...
But it's there now, and I'll be interested to see if it's of use to JTSer's. There seems to be a sudden surfeit of Delaunay and CDT Java libraries (see here, here, here, here and here), so I make no claims that the JTS one is best-of-breed. But hopefully having a decent implementation easily accessible and embedded in a general-purpose library will meet some needs. Also, my hope is that it will serve as the basis for further algorithms in JTS (such as the much-sought-after Concave Hull!).
Here's some screenshots showing the triangulation API at work:
The input points and constraint segments:
The Delaunay triangulation (notice that triangle edges cross some of the longer constraint edges):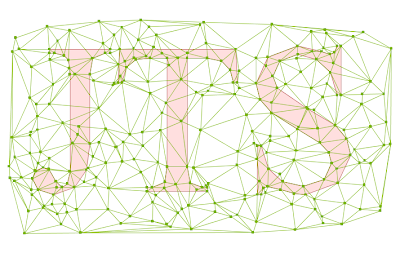
A conforming Delaunay triangulation (the triangulation edges are now faithful to the constraint edges):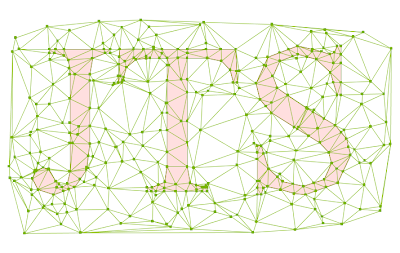
8 comments:
great! thanks Martin. I guess it will sooner or later make its way into OpenJUMP (the questions is in which enduser friendly application way). But research will pick it up for sure.
Hello.
Thank you for your great work.
Are you interested in Generalized Voronoi Diagrams/Algorithms as follows.
-http://www.nirarebakun.com/voro/voro.html (Sorry in Japanese and too heavy)
-Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware: http://www.cs.unc.edu/~geom/voronoi/
Regards.
Hi Martin
Curious - whatever became of your WaterBuG application? Never was able to find a copy of your presentation from FOSS4G 07 or GeoTec07 anywhere online - just a couple of "teaser mentions" here & there. Is WaterBuG still alive ? If so, any information available about it? Would it be possible to use it on USGS NHD format stream network data ?
Thanks,
Julia
Julia,
WaterBuG is alive and well, but not leading a very exciting life these days. It is being used in production for computing watersheds for the BC stream network, and has worked well for that application. As long as there was a suitable driver to read the USGS data, I expect it would be able to run on it as well.
You're right about there being a lack of information & code available, though. As you know, it takes a bit of effort to package up an application along with documentation to make it usable by a wider audience. Unfortunately the client sort of lost interest in doing this, and we haven't devoted the time to doing so up til now.
I can provide the presentation easily - in fact, I'll make it available online. The source could be available too - with the proviso that it will probably need some work to make the inputs & outputs more generally usable. What I'd like to do is to provide WaterBuG as a JEQL extension - that will make it much more easily configurable for inputs, outputs and parameters.
Feel free to contact me directly for more info.
Hello Martin,
When is version 1.11 going to be released? My interest is in nterpolating surface with a VERY large number of data points, using the Delaunay triangulation.
Thanks,
Alex Molochnikov
Kelman Technologies Inc.
Hi Martin,
Thanks for this amazing JTS package! I have tested it. It is easy to use and very quick.
However, I did not find how to compute a conforming Delaunay triangulation without creation of new points on the constraint edges. I know in this case the triangulation is no more a 'Delaunay' triangulation, but is it possible to get it?
JTS will compute a conforming Delaunay Triangulation. This is a true Delaunay, but which necessarily introduces new Steiner points along edges. There is also a notion of a constrained Delaunay, which isn't true Delaunay but which doesn't split edges. JTS does not have code to compute this.
Thanks for your answer!
Post a Comment